График сечений функции невязки f (х) = |Ахb|
Рисунок 8.8. График сечений функции невязки f (х) = |Ах-b|
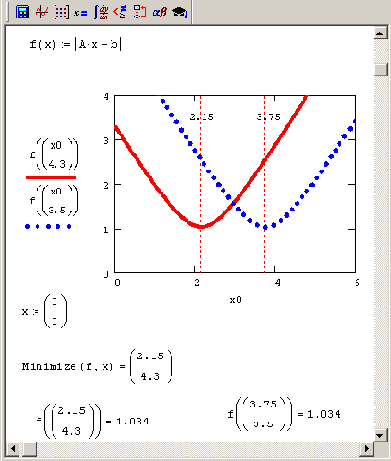
Несложно догадаться, что в рассматриваемом сингулярном случае псевдорешений системы, минимизирующих невязку |Ax-b|, будет бесконечно много, и лежать они будут на третьей прямой, параллельной двум показанным на Рисунок 8.7 и расположенной в середине между ними. Это иллюстрирует Рисунок 8.8, на котором представлено несколько сечений функции f(x)= = | Аx-b |, которые говорят о наличии семейства минимумов одинаковой глубины. Если попытаться использовать для их отыскания встроенную функцию Minimize, ее численный метод будет всегда отыскивать какую-либо одну точку упомянутой прямой (в зависимости от начальных условий). Поэтому для определения единственного решения следует выбрать из всего множества псевдорешений то, которое обладает наименьшей нормой. Можно пытаться оформить данную многомерную задачу минимизации в Mathcad при помощи комбинаций встроенных функций Minimize, однако более эффективным способом будет использование регуляризации (см. ниже) или ортогональных матричных разложений (см. разд. 8.3).
Плохо обусловленные системы
Плохо обусловленная система — это система, у которой определитель А не равен нулю, но число обусловленности |А-1| |А| очень велико. Несмотря на то, что плохо обусловленные системы имеют единственное решение, на практике искать это решение чаще всего не имеет смысла. Рассмотрим свойства плохо обусловленных СЛАУ на двух конкретных примерах (листинг 8.14).
