К пояснению задач поиска локального и глобального экстремума
Рисунок 6.1. К пояснению задач поиска локального и глобального экстремума
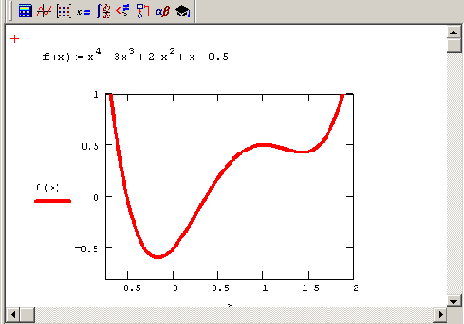
Общая проблема поиска экстремума функции включает в себя задачи нахождения локального и глобального минимума. Последние называют еще задачами оптимизации, и решить их, как правило, намного труднее, поскольку они подразумевают локализацию всех минимумов f (х) и выбор из них наименьшего. (На Рисунок 6.1 показаны два локальных минимума функции, из которых левый является глобальным.) Ограничения значений аргументов, задающих область определения f (х), как и прочие дополнительные условия, могут быть определены в виде системы неравенств и (или) уравнений. В таком случае говорят о задаче на условный экстремум.
Численные методы, применяемые для минимизации, сходны с методами решения нелинейных уравнений, и поэтому материал этой главы близок по содержанию к предыдущей.
Примечание 1
Примечание 1
Решение задач минимизации в Mathcad реализовано только при помощи численного алгоритма. Таким образом, непосредственное символьное нахождение минимума невозможно. Однако аналитический поиск экстремума функции несложно запрограммировать, опираясь на соответствующие сведения математического анализа (см. разд. 6.1.5).
