Реализация алгоритма прямоугольников
Рисунок 4.4. Реализация алгоритма прямоугольников
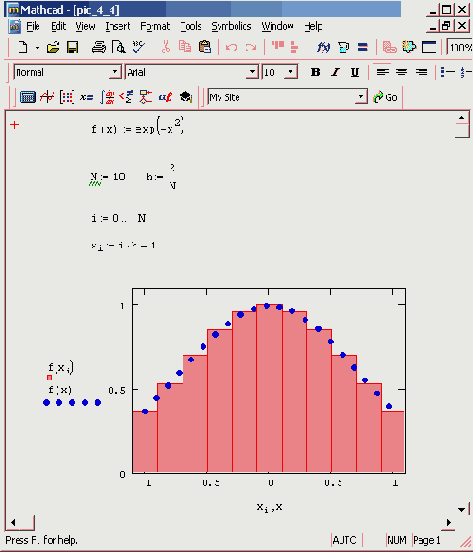
Очевидно, что наиболее простой алгоритм заключается в интерполяции подынтегральной функции на каждом из N шагов интегрирования f (х) каким-либо полиномом у(х). Известно, что могут быть предложены различные пути построения интерполирующих полиномов, отличающихся, в частности, порядком. Например, полиномы Лагранжа строятся при интерполяции f (х) в n точках на каждом из N элементарных интервалов интегрирования. Семейство классических алгоритмов интегрирования в этом случае называется методами Ньютона—Котеса. Заметим, что при n=1 полиномом является прямая линия, и мы имеем метод трапеций; при n=2 интерполирующим полиномом на каждом шаге интегрирования будет квадратичная парабола, и мы получим алгоритм Симпсона и т. д.
Примечание 1
Примечание 1
Дополнительные сведения об алгоритме полиномиальной интерполяции приведены в главе 13.
