Численное и символьное
Листинг 3.9. Численное и символьное вычисление шестой производной
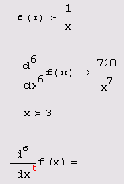
Чтобы вычислить производную порядка выше 5-го численно, можно последовательно применить несколько раз оператор м-й производной (листинг 3.10), подобно тому, как производится отыскание кратных интегралов (см. разд. 4.3.4). Однако следует помнить о том, что численное определение производных высших порядков производится тем же вычислительным методом Риддера, что и для первых производных. Поскольку, как уже было сказано, для первой производной этот метод обеспечивает точность до 7—8 значащих разрядов числа, при повышении порядка производной на каждую единицу точность падает примерно на один разряд.
ВНИМАНИЕ!
Из сказанного ясно, что падение точности при численном расчете высших производных может быть очень существенно. В частности, если попытаться определить шестую производную функции l/х, то в качестве результата будет выдан ноль, в то время как истинное значение девятой производной может быть найдено при помощи символьного процессора (листинг 3.10).
