Двумерный массив (матрица)
Листинг 1.15. Двумерный массив (матрица)
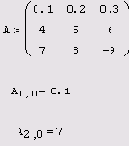
Доступ ко всему массиву осуществляется обычным поименованием векторной переменной. Над элементами массива можно совершать действия, как над обычными числами. Нужно только правильно задать соответствующий индекс или сочетание индексов массива. Например, чтобы получить доступ к нулевому элементу вектора а из листинга 1.14:
1. Введите имя переменной массива (а).
2. Нажмите кнопку Subscript (Нижний индекс) со значком х„ на панели Matrix (Матрица), либо введите [.
3. В появившийся справа снизу от имени массива местозаполнитель введите желаемый индекс (0).
Если после этого ввести знак численного вывода, то справа от него появится значение нулевого элемента вектора, как показано во второй строке листинга 1.14.
Чтобы получить доступ к элементу многоиндексного массива (например, элементу a1,0 матрицы а из листинга 1.15):
1. Введите имя переменной массива (а).
2. Перейдите к вводу нижнего индекса, введя [.
3. Введите в местозаполнитель индекса первый индекс (2), запятую (,) и в появившийся после запятой местозаполнитель введите второй индекс (0).
В результате будет получен доступ к элементу, как показано в последней строке листинга 1.15.
Примечание 1
Примечание 1
В рассмотренных листингах нумерация индексов массивов начинается с нуля, иными словами, первый элемент массива имеет индекс 0. Стартовый индекс массива задается системной переменной ORIGIN, которая по умолчанию равна нулю. Если вы привыкли нумеровать элементы векторов и матриц с единицы, присвойте этой переменной значение 1. Обратите внимание, что в этом случае попытка выяснить значение нулевого элемента вектора приводит к ошибке, поскольку его значение не определено.
Примечание 2
Примечание 2
Помимо доступа к отдельным элементам массива, имеется возможность совершать действия над его подмассивами (например, векторами-столбцами, образующими матрицу). Делается это с помощью оператора со значком х<>
на панели Matrix (Матрица) (листинг 1.16). Символ "Т" во второй строке листинга 1.16 обозначает операцию транспонирования матрицы.
