Балансовые показатели
Ниже приводится ряд раскрасок карты Кохонена Российских банков по некоторым статьям баланса. Как видно из карт Итого доходов и Итого расходов, наиболее активные банки (банки, у которых отношение доходов и расходов к их размеру наибольшее) располагаются в левом верхнем углу карты. Карта размеров говорит нам о том, что эти банки относительно невелики по своим размерам.
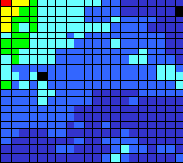
Рис. 10.12. Итого доходов
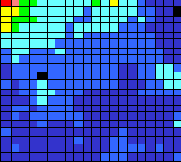
Рис. 10.13. Итого расходов
Очень показательны карты Всего обязательств и Прибыль/убыток. Из карты Прибыль/убыток ясно видно, что наиболее убыточной является группа банков-банкротов (правый верхний угол). Эта же группа банков имеет больше всего обязательств.

Рис. 10.14. Прибыль/убыток
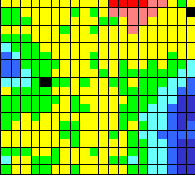
Рис. 10.15. Всего обязательств
Интересно отметить, что меньше всего обязательств имеют обе группы малых банков. Эти группы банков сходны по многим параметрам (на карте Уставной фонд видно, что у малых банков отношение уставного фонда к размеру выше, чем у остальных). Однако, как видно из карты Прибыль/убыток, в отличие от группы малых банков слева, которая является самой прибыльной, группа справа имеет прибыль ниже среднего. Это говорит о том, что скорее всего деятельность этих групп имеет разные цели. Малая прибыль в совокупности с большим уставным фондом и малыми обязательствами говорит о том, что банки из группы справа скорее всего служат для расчетных операций различных организаций, а не для получения прибыли.
Данные о российских банках
Для иллюстрации описываемого подхода далее в этой
лекции 1) будут использованы данные Центрального Банка России о годовых балансах и отчетах о прибылях/убытках примерно 1800 российских банков за 1994, 1995 годы, предоставленные информационным агентством "Прайм". Каждый банк при этом описывается 30 финансовыми показателями - отношением балансовых статей к общей сумме активов банка. Подобная нормализация приводит все статьи к единому масштабу, сглаживая различия между крупными и мелкими банками, составляющие несколько порядков величин. Из этих 30 параметров нам предстоит оптимальным образом сконструировать две обобщенные координаты.
Исторические корни
Пионерская работа Альтмана в этом направлении датируется 1968 годом (Altman, 1968). Используя метод линейного дискриминантного анализа он выявил пять наиболее значимых финансовых индикаторов, влияющих на предсказание банкротств:
(Оборотные средства / Общий размер активов) - характеризует денежные активы фирмы, т.е. ее способность мобилизовать ресурсы для немедленной уплаты долгов. (Нераспределенная прибыль / Общий размер активов) - прибыль после уплаты налогов и выплат акционерам, которая остается в распоряжении корпорации, например, для реинвестирования, характеризует источник погашения долгов. (Прибыль до выплаты налогов и процентов по вкладам / Общий размер активов) - характеризует общую эффективность управления капиталом. (Рыночная капитализация / Общий размер долгов) - характеризует отношение собственного капитала к заемному, т.е. эффективный размер долга. (Объем продаж / Общий размер активов) - характеризует активность использования фирмой своих ресурсов.
В последующих работах разные авторы дополняли или видоизменяли список ключевых финансовых индикаторов по своему усмотрению. Наиболее общий подход, видимо, состоит в использовании в качестве входов логарифмов укрупненных статей балансов и отчетов о прибылях/убытках. Нейросеть в этом случае сама выберет наиболее значимые линейные комбинации входов, которым будут соответствовать наиболее значимые отношения различных статей в нужных пропорциях. Использование индикаторов, с другой стороны, помогает в интерпретации результатов нейро-моделирования если воспользоваться, например, техникой прореживания связей и извлечения правил, описанной в предыдущей лекции. Заметим, что использование описанных выше индикаторов лежит также в основе общепринятой методики рейтингования банков CAMEL.
Карта размеров банков
Рассмотрим, например как располагаются на построенной карте банки разных размеров (см. рисунок 10.10
). 1)
Размеры банков берутся в логарифмической шкале, причем клетки, отличающиеся на одну цветовую градацию, содержат банки с пятикратным отношением активов. Напомним, что величин активов банков была изначально выведена из набора параметров, т.к. она использовалась для нормировки остальных статей. Несмотря на это, банки разных размеров располагаются не хаотично, а регулярным образом, что свидетельствует о значимости размера банка при выборе им своей финансовой стратегии. Визуально на карте можно выделить следующие большие группы банков: большие банки (низ карты), малые банки (группа слева и группа справа) и средние банки. Раскраска, отражающая относительный размер Уставного фонда показывает, что между двумя группами малых банков имеются существенные различия: Банкив нижнем правом углу карты практически не растут ( рисунок 10.11).
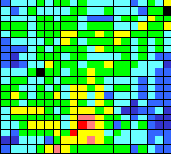
Рис. 10.10. Размер активов российских банков
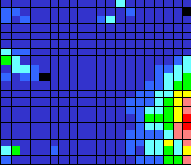
Рис. 10.11. Уставной фонд
Сравнение с расположением банков-банкротов, показывает, что вероятность банкротства как больших так и малых банков в 1994 году была невелика.
Линейное сжатие информации - метод главных компонент
Более общий подход - использовать не две отдельные компоненты, а две линейные комбинации всех 30 исходных параметров, наилучшим образом представляющие имеющиеся данные (см. рисунок 10.3).
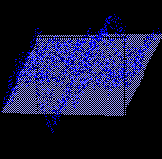
Рис. 10.3. Линейная аппроксимация многомерных (здесь - трехмерных) данных
Каждый банк представлен точкой в 30-мерном пространстве и задача состоит в проведении двумерной плоскости в этом пространстве, обеспечивающей минимальное среднеквадратичное отклонение имеющихся точек от этой плоскости:

Как мы знаем подобное линейное приближение дается методом главных компонент. Если действительное расположение точек не сильно отклоняется от плоскости, этот метод может дать неплохое начальное приближение. Однако, оказывается, что в даном случае это не так. Среднеквадратичное отклонение для случая двух главных компонент оказалось равным почти половине от общей дисперсии:

Таким образом, даже оптимальный вариант линейного сжатия не дает возможности визуализировать финансовое положение банков. Оно может, тем не менее, оказаться полезным, в частности, для анализа значимости балансовых статей. Так, увеличение числа главных компонент постепенно дает все лучшее и лучшее приближение имеющегося массива данных (см. Ошибка! Источник ссылки не найден.).
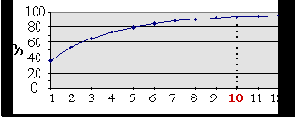
Рис. 10.4. Точность воспроизве-дения данных как функция числа главных компонент
Например, 10 главных компонент обеспечивают вполне приемлемую общую точность 94% (т.е.

Степень восстановления исходных данных по ограниченному числу главных компонент свидетельствует о том, насколько согласованны данные в этих статьях между собой во всем массиве имеющейся информации, т.е. насколько содержащаяся в них информация значима для выявления индивидуальных отличий. Ошибка! Источник ссылки не найден. показывает, что около 20 статей восстанавливаются по 10 главным компонентам с относительно высокой точностью. Это как раз те статьи, кторые дают основной вклад в главные компоненты. Остальные статьи гораздо менее значимы для сравнительного финансового анализа, в частности, в силу незначительности совокупной доли активов в этих статьях балансов.
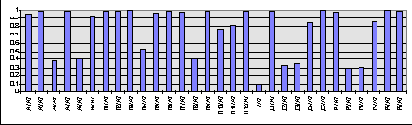
Рис. 10.5. Значимость статей балансов и отчетов о прибылях/убытках, определенная по степени их восстановления по 10 главных компонентам
Нейросетевое предсказание банкротств
Обобщая опыт сравнительного анализа предсказаний банкротств различными методиками (Trippi, Turban, 1993), отметим:
Нейросетевое моделирование обеспечивает наилучшую точность предсказания банкротств: порядка 90%, по сравнению с 80%-85% точностью для других статистических методик (дискриминантный анализ, логистический анализ, ID3, kNN). При желании можно повысить "подозрительность" нейросети, обеспечив точность выявления банкротов вплоть до 99% - за счет снижения требований к ошибкам второго рода (класификации нормальной фирмы как банкрота). Это достигается путем увеличения веса ошибки первого рода (класификации банкрота как нормальной фирмы). В зависимости от конкретной практической задачи "подозрительность" сети можно произвольно регулировать. Банкротства можно уверенно предсказывать за несколько лет до их фактического наступления, причем точность предсказания за два года практически не отличается от точности предсказания за год. Таким образом, неявные сигналы неблагополучия присутствуют в финансовой отчетности фирмы задолго до ее краха.
Нелинейное сжатие информации - карты Кохонена
Итак, линейная статистическая обработка данных не способна выделить два ведущих параметра, описывающих финансовое состояние российских банков с приемлемой точностью. В этой ситуации естественно обратиться к нелинейному статистическому анализу, т.е. к нейросетевому моделированию.
Напомним, что методом, дающим оптимальное представление информации в виде координат двумерной сетки, является построение топографических карт (карт Кохонена), о которых шла речь в лекции 4. Напомним в двух словах суть этой методики. В многомерное пространство данных погружается двумерная сетка. Эта сетка изменяет свою форму таким образом, чтобы по возможности точнее аппроксимировать облако данных. Каждой точке данных ставится в соответствие ближайший к ней узел сетки. Таким образом каждая точка данных получает некоторую координату на сетке. Такое отображение локально непрерывно: близким точкам на карте соответствуют близкие точки в исходном пространстве (обратное, вообще говоря, не верно: близким точкам в исходном пространстве могут соответствовать далекие точки на карте - такова цена понижения размерности). Таким образом, распределение данных на двумерной карте позволяет судить о локальной структуре многомерных данных.
Синаптические веса нейрона в сети Кохонена являются его координатами в исходном многомерном пространстве. Обучение сети, т.е. нахождение положения узлов карты в многомерном пространстве происходит в режиме "победитель забирает все". Данные по очереди подаются на входы всех нейронов и для каждого входа определяется ближайший к нему нейрон. Обучение состоит в подгонке весов нейрона-победителя и его ближайших соседей минимизурующих отклонение данных от нейронов-победителей. Постепенно сеть находит равновесное положение, оптимально аппроксимирующее данные (см. рисунок 10.6).
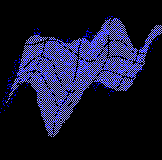
Рис. 10.6. Нелинейная аппроксимация массива многомерных данных двумерной поверхностью
Если линейный статистический анализ пытается аппроксимировать данные плоскостью, то нелинейный - использует для этих целей двумерную поверхность, что позволяет, в принципе, добиться гораздо более высокой точности аппроксимации.
Так, в нашем случае, суммарное расстояние от данных до ближайших к ним узлов топографической сетки

составляет всего


Таким образом, можно с приемлемой точностью описать финансовое состояние российских банков используя всего лишь два обобщенных финансовых индикатора, а именно - две координаты на двумерной карте Кохонена. Каждый банк по состоянию своего баллансового отчета отображается конкретной ячейкой на карте. Ячейки с одинаковыми координатами содержат банки со сходным финансовым состоянием. Чем дальше на карте координаты банков, тем больше отличается друг от друга их финансовый портрет.
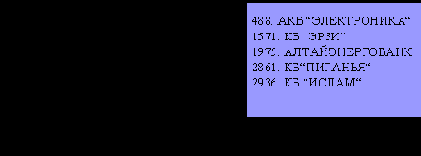
Рис. 10.7. Пример содержимого ячейки Т9 карты Кохонена для российских банков (регистрационные номера и названия банков)
Так, например, рисунок 10.7 иллюстрирует содержимое конкретной ячейки на карте Кохонена российских банков, содержащей 20x20 ячеек (т.е. 400 нейронов).
Обсуждение
Полезность обучения сети на примерах обанкротившихся фирм состоит также в том, что такая сеть вырабатывает дискриминантную функцию - численный показатель финансового здоровья фирмы, меру ее устойчивости. Однако, устойчивость не является единственным возможным критерием оценки деятельности
фирмы. 1) Акционеры, например, заинтересованы не только в бесконечно долгом существовании фирмы, но и в получении достаточно весомой прибыли. Важно, кроме того, не только состояние фирмы на настоящий момент, но и характеристики существующих тенденций. Здесь значимым может оказаться другой набор факторов, дающий другую оценочную функцию. Так, высокая доходность может обеспечить повышение надежности в будущем. Между тем, неясно каким образом можно обучать нейросеть на "будущий успех" при отсутствии такого же четкого критерия успеха, каким является банкротство для неудачи.
Эти объективные трудности можно преодолеть, если вспомнить, что фирма существует не сама по себе, а в сообществе подобных ей фирм-конкурентов. И именно в сопоставлении с этим сообществом можно говорить о сильных и слабых сторонах ее деятельности. Эти рассуждения подводят нас к другой постановке задачи: комплексной оценки финансового состояния фирмы путем систематического сравнения ее показателей с показателями остальных участников данного рынка. Такой подход, рассмотренный в следующем разделе, не требует знания готовых ответов, т.к. основан на обучении без учителя.
Полезность обучения сети на примерах обанкротившихся фирм состоит также в том, что такая сеть вырабатывает дискриминантную функцию - численный показатель финансового здоровья фирмы, меру ее устойчивости. Однако, устойчивость не является единственным возможным критерием оценки деятельности
фирмы. 4) Акционеры, например, заинтересованы не только в бесконечно долгом существовании фирмы, но и в получении достаточно весомой прибыли. Важно, кроме того, не только состояние фирмы на настоящий момент, но и характеристики существующих тенденций. Здесь значимым может оказаться другой набор факторов, дающий другую оценочную функцию. Так, высокая доходность может обеспечить повышение надежности в будущем. Между тем, неясно каким образом можно обучать нейросеть на "будущий успех" при отсутствии такого же четкого критерия успеха, каким является банкротство для неудачи.
Эти объективные трудности можно преодолеть, если вспомнить, что фирма существует не сама по себе, а в сообществе подобных ей фирм-конкурентов. И именно в сопоставлении с этим сообществом можно говорить о сильных и слабых сторонах ее деятельности. Эти рассуждения подводят нас к другой постановке задачи: комплексной оценки финансового состояния фирмы путем систематического сравнения ее показателей с показателями остальных участников данного рынка. Такой подход, рассмотренный в следующем разделе, не требует знания готовых ответов, т.к. основан на обучении без учителя.
Приведенные выше раскраски в совокупности образуют атлас, отражающий финансовое состояние банков или других фирм, занимающихся сходными видами бизнеса. Этот атлас дает графическое отображение положения любой конкретной фирмы среди конкурентов и может использоваться как удобное средство финансового анализа. В частности, можно рассматривать эволюцию финансового положения отдельной фирмы во времени, выявлять существующие тенденции и циклы. С точки зрения макроэкономики удобство такого рода карт состоит в том, что площади на этой карте примерно пропорциональны доле фирм в силу более-менее равномерного заполнения ячеек. Таким образом можно зримо представлять себе, например, долю крупных банков или банков, испытывающих трудности с возвратом кредитов.
Оценка акций
В отличае от облигаций, являющихся своего рода долговыми расписками, акции корпораций не гарантируют возврата процентов и основной суммы долга. Однако, оценка перспективности различных активов в пакетах акций является одной из главных задач любого инвестора. Ранее мы описывали возможности предсказания котировок акций в будущем, основанные на анализе прошлого поведения временного ряда котировок. Альтернативный подход представляет собой рейтингование акций, основанное на более широком круге финансовых показателей компаний, доступных из их финансовых отчетов.
Результативность подобного подхода иллюстрируют рейтинги ведущего консультационного агентства США по инвестициям в акции - Value Line. Раз в неделю это агентство разбивает акции около 1700 компаний по 5 рейтинговым категориям (алгоритм, естественно, широкой публике неизвестен). Статистические исследования подтверждают значимость рейтинга Value Line. А именно, пакеты, составленные из акций более высокой рейтинговой категории, систематически дают большую прибыль в течении ближайшего квартала (в следующем квартале эффект уже заметно меньше).
Есть основания предполагать, что квартальные отчеты корпораций влияют на курс акций. В частности, неожиданно высокие прибыли (убытки) статистически значимо коррелируют с повышением (понижением) курсов
акций. 3)
Причем, эта корреляция существует достаточно долго - в течении по крайней мере двух месяцев со дня публикации отчета. Следовательно, инвестор имеет возможность извлечь определенную выгоду из финансовой отчетности корпораций. Справедливости ради следует отметить, что такая же корреляция имеется и на протяжении двух месяцев до объявления о прибылях/убытках (Шарп, и др. 1997). Это означает, что информация о состоянии фирмы просачивается на рынок раньше официальной публикации, так что временной ряд уже содержит эту информацию в неявном виде. Однако, интерпретация финансовых показателей отчета может дать гораздо более содержательную информацию, чем динамика временного ряда, зашумленная многими внешними факторами.
В более общей постановке речь идет о прогнозировании финансового "здоровья" корпорации на основании ее финансовой о тчетности. Нетривиальным моментом здесь является количественное определение финансового благополучия. Можно, как и в случае с облигациями, воспользоваться для обучения сети рейтингами, например, упомянутого выше агентства Value Line для воспроизведения этой, в общем-то субъективной оценки компании. Можно попытаться использовать в качестве индикатора благополучия более объективный критерий - рыночный курс акций в ближайшем или более отдаленном будущем (Бэстенс и др., 1997). Однако, рыночный курс может быть подвержен сильным флуктуациям чисто спекулятивного характера. Наконец, можно воспользоваться указаниями самого сурового учителя, исследуя крайнюю форму проявления финансового "недомогания" - банкротство. Анализ банкротств, таким образом, может служить источником объективных оценок устойчивости финансового положения фирм.
Постановка задачи
С математической точки зрения эта задача сводится к оптимальному сжатию информации о финансовом состоянии фирмы, т.е. отображении информации минимальным числом параметров при заданном уровне огрубления или минимизации потерь информации при заданном числе обобщенных координат. Для целей визуализации, выгодно ограничиться двухпараметрическим представлением. Это уже существенный шаг вперед по сравнению с однопараметрическим рейтингом.
Предсказание рисков банкротств
Сначала приведем несколько цифр, иллюстрирующих "цену вопроса". Мировой рынок только межбанковских кредитов оценивается в $38 трлн. Это почти в два раза превышает мировой объем ценных бумаг. Естественно, что оценка риска невозврата кредитов имеет для банков первостепенное значение. (В случае страховки, этот риск, перекладывается на страховщика. Общий объем страховых премий в этой индустрии риска составляет $2.5 трлн.)
Количество банкротств в США на протяжении 80-х годов возрастало ежегодно примерно на 14%. В банковском секторе США число банкротств возросло с 50 в 1984 г. до 400 в 1991 г. Это, однако, составляет менее 3% от примерно 14000 действующих в США банков. В России же, например, только в 1996 г. лицензии были отозваны более чем у 10% из около 2000 зарегистрированных банков. Таким образом, предсказание банкротств, особенно в кризисных экономических условиях, является насущной задачей экономического анализа.
Если в проблеме рейтингования задачей нейросети было воспроизвести мнения экспертов о надежности корпорации, то нейросетевое предсказание банкротств основано на статистической обработке конкретных примеров банкротств. В такой постановке задача нейросети - самой стать экспертом, определяющим финансовую стабильность корпорации, основываясь исключительно на объективной информации - показателях финансовой отчетности. Обычно от нейросети требуется оценить вероятность банкротства через определенный промежуток времени (например, через год или через два года) по доступной на данный момент финансовой отчетности. В качестве входов используют финансовые индикаторы - отношения балансовых статей, наиболее полно отражающие определенные стороны финансового положения фирмы.
Раскраски карты Кохонена
Различные раскраски топографической карты являются удобным средством для выявления взаимосвязей различных факторов. В принципе, любая финансовая характеристика порождает свою раскраску карты, как это иллюстрирует рисунок 10.9.
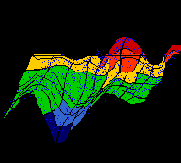
Рис. 10.9. Раскраска карты, порожденная -ой статьей баланса
Вместе подобные раскраски дают исчерпывающую и наглядную картину. Здесь имеется полная аналогия с географическими картами различных типов на одной и той же географической сетке, которые в совокупности дают полное представление о данной местности.
Расположение на карте банков с отозванной лицензией
Достоинства карты Кохонена начинают проявляться после нанесения на нее какой-либо графической информации. рисунок 10.8 показывает как выглядит карта Кохонена, на которой отмечены ячейки, содержащие банки с отозванными по результатам 1994 года лицензиями. Видно, что банки с отозванными лицензиями группируются в правом верхнем углу карты - "зоне риска". Мы увидим, что эта зона имеет и другие признаки неблагополучия.

Рис. 10.8. Ячейки, содержащие хотя бы один банк с отозванной в 1994 году лицензией
Отметим, что в отличие от анализа банкротств, описанного в первой части лекции, здесь информация о банкротствах не участвовала в обучении сети. Она изображена на уже готовой карте, являсь лишь индикатором области параметров с повышенным риском банкротства. Эта особенность описываемой методики позволяет выявить область риска по относительно небольшому числу примеров (как в нашем случае).
Рейтинг корпоративных облигаций
Существенную часть рынка ценных бумаг составляют корпоративные облигации - займы корпораций под фиксированный процент. Только на Нью-Йоркской Фондовой бирже в 1992 г. обращались облигации около 1500 компаний с общей номинальной стоимостью свыше $260 млрд. Для оценки риска невыплаты процентов или невозврата денег по облигации практически для всех таких корпораций существуют и периодически обновляются рейтинги, составляемые независимыми рейтинговыми агентствами.
В рейтинговом бизнесе доминируют две компании: Standard & Poor's и Moody's. Свыше 2000 долговых эмитентов поставляют свои финансовые отчеты этим двум организациям. Рейтинги этих агентств чрезвычайно авторитетны, от них напрямую зависят процентные ставки по облигациям: чем ниже рейтинг эмитента - тем дороже обходится эмитенту обслуживание своего долга, т.к. инвесторы желают получить плату за дополнительный риск. Более того, в США некоторым категориям инвесторов, таким, как банки и страховые компании, законодательно запрещено покупать облигации с рейтингом Standard & Poor's и Moody's ниже определенного уровня. Так, в классификации Standard & Poor's (таблица 10.1) бумаги с рейтингом ниже BBB считаются в основном спекулятивными. Их характеризует большая степень неопределенности в возможности выплаты процентов и возвращения основного долга (рейтинг России также принадлежит пока к этой
категории. 1)
| AAA | Самая высокая вероятность выплаты процентов и возврата долга | 0.00% |
| AA | Высокая вероятность выплаты процентов и возврата долга | 1.70% |
| A | Высокая вероятность выплаты процентов и возврата долга, но несколько большая зависимость от экономической коньюнктуры | 0.65% |
| BBB | Адекватная вероятность выплаты процентов и возврата долга, еще большая зависимость от неблагоприятных факторов | 1.54% |
| BB | Долговые обязательства, хотя и имеют защитные характеристики, но характеризуются огромной неопределенностью невыплаты процентов | 5.93% |
| B | 20.87% | |
| CCC | 38.08% |
Чтобы составить представление о степени риска, характерном для облигаций с различными рейтингами, в последнем столбце этой таблицы приведены данные исследований реальных неплатежей по корпоративным облигациям в течении двадцати лет (Altman, 1991), а именно: процент бумаг, по которым в течении первых пяти лет с момента их выпуска были отмечены неплатежи. Можно отметить действительно отчетливую границу между "надежными" и "рискованными" облигациями.
Алгоритм составления описанных выше рейтингов неизвестен, более того, агентства утверждают, что он не основан в чистом виде на статистическом анализе финансовой информации, а содержит еще оценки экспертов, например для таких трудно формализуемых параметров, как "качество менеджмента". Такая ситуация вполне устраивает сами рейтинговые агентства, превращая их продукцию в уникальный товар. Однако многие инвесторы заинтересованы в обладании своими собственными алгоритмами рейтингования, "эмулирующими" рейтинги большой двойки - по крайней мере по трем причинам.
Во-первых, не для каждой облигации имеется официальный рейтинг. Многие бумаги, обойденные вниманием крупных рейтинговых агентств, могут в итоге оказаться весьма привлекательными для инвестиций, если суметь грамотно оценить степень их рискованности. Во-вторых, обновление официальных рейтингов происходит не столь часто, как хотелось бы. Умение загодя, до того как это станет общедоступной информацией, предугадать изменение рейтингов, очевидно, дает инвесторам дополнительные конкурентные преимущества. Наконец, разгадав стратегию "официального" рейтингования, инвесторы могут надеяться улучшить качество оценки финансового состояния эмитентов путем более интенсивного статистического анализа, получив, таким образом, преимущество над теми, кто пользуется официальными рейтингами.
Приведенные выше доводы обосновывают следующую постановку задачи для нейро-анализа: на основе общедоступной финансовой отчетности компаний-эмитентов постараться воспроизвести рейтинги Standard & Poor's и/или Moody's.
Несмотря на наличие неформальной компоненты, представляется вероятным, что алгоритмическая составляющая этих рейтингов довольно велика. В конце концов, общая численность аналитиков в обоих ведущих агентствах вместе взятых не превышает 100 человек. Так что справиться с обработкой постоянно обновляемых данных о 2000 эмитентах они могут лишь используя в основном автоматизированные процедуры.
Попытки смоделировать алгоритм рейтингования облигаций предпринимались с 60-х годов (Horrigan, 1966) и базировались на методе линейной регрессии. Типичный процент угадывания рейтинга в этих моделях составляет примерно 60%. Поскольку возможности нелинейного нейросетевого моделирования шире, неудивительно, что первые же попытки применить нейросети показали существенно лучшие результаты - на уровне 88% для воспроизведения отдельной градации рейтинга (Dutta, Shekhar,
1988). 2)
Более сложные нейросетевые модели способны с приемлемой точностью воспроизводить широкий диапазон рейтингов облигаций по набору ключевых финансовых индикаторов фирм-имитентов. Например, в работе (Moody, Utans, 1993) 97% предсказаний нейросети расходятся не более чем на один пункт с классификацией Standard & Poor's в интервале [AAA+AA, A, BBB, BB, B] .
Заметим, что несмотря на неплохие, в общем-то, результаты, подобные нейросетевые модели весьма компактны. В качестве входных переменных обычно используется от 6 до 10 финансовых индикаторов, являющихся отношением наиболее значимых статей балансов и отчетов о прибылях и убытках корпораций. Например, в последней из упомянутых выше работ первоначально использовались 10 финансовых индикаторов, отобранных аналитиками одного из крупных американских банков. Однако по результатам анализа чувствительности нейросетевых предсказаний к входным переменным два из этих индикаторов оказались незначимыми и не использовались в окончательной модели (8-3-1 персептрон с 3 нейронами на скрытом слое и 1 выходным линейным нейроном, дающим численный эквивалент рейтинга).Качество воспроизведения "тонких" градаций (с учетом субкатегорий, например AA+, AA-) рейтинга агентства Standard & Poor's, достигнутое этой моделью, иллюстрирует рисунок 10.1.
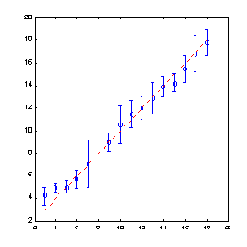
Рис. 10.1. Воспроизведение 15-ти градаций рейтинга Standard & Poor's (штриховая линия) в работе (Moody, Utans, 1993)
Сечения
Главный вопрос теперь - как выбирать эти обобщенные координаты. Можно, например, воспользоваться сечениями имеющихся многомерных данных, иными словами - просто выбрать два "наиболее важных" с точки зрения экспертов параметра балансов и таким образом отобразить на двумерной карте положение всех фирм. Для российских банков подобное представление информации практикует журнал "Эксперт" (см рисунок 10.2).

Рис. 10.2. Положение пятнадцати крупнейших российских банков в 1996 г. в координатах "Надежность" - Доходность. (По материалам журнала "Эксперт")
Согласно такому подходу надежность банка характеризуется одним финансовым показателем - отношением собственного капитала к привлеченному. В первой половине этой лекции мы видели, однако, что анализ банкротств выявляет как минимум пять (а то и восемь) значимых финансовых показателей, влияющих на надежность.
Сравнительный анализ финансового состояния фирм
Сравнительный анализ, в отличае от рейтингования, предполагает введение не одной, а нескольких оценочных координат. Это позволяет лучше использовать имеющуюся информацию, более точно позиционировать фирму среди остальных. С другой стороны, для обозримости результатов сравнительного анализа, количество параметров сравнения должно быть по возможности минимальным. В узком смысле "обозримость" требует введения не более двух координат - чтобы относительная позиция фирмы могла быть представлена точкой на двумерной карте, а различные финансовые показатели могли быть визуализированы в виде двумерных поверхностей.
предсказание рисков
Существуют две базовые инвестиционные стратегии: активная, основанная на предсказаниях доходности тех или иных активов, и пассивная, в которой рынок полагают непредсказуемым, и главной целью ставят минимизацию рисков. Оценка инвестиционного риска, таким образом, является одним из краеугольных камней финансового анализа. В этой лекции рассмотрены основные нейросетевые методики оценки рисков и составления рейтингов.
Эти методики используют два основных подхода: обучение с учителем - на примерах экспертных оценок или обанкротившихся фирм, и обучение без учителя - путем категоризации имеющихся данных. Сначала рассмотрим первый, более прямолинейный подход.
В данной лекции были рассмотрены
В данной лекции были рассмотрены различные подходы к анализу рисков. Одни из них в для формирования обучающей выборки используют мнения авторитетных рейтинговых агентств, другие - опираются на объективные данные о банкротствах. Наконец, альтернативный подход использует для обучения сети "непомеченные" финансовые данные, предлагая методику сравнительного финансового анализа.
Адаптация функций принадлежности
В лекции, посвященной извлечению знаний из обученных нейронных сетей, мы познакомились с методами интерпретации отображения сетью входной информации в выходную с помощью правил типа неравенств, правил m-of-n и других. В теория нечетких множеств соответствующие нечеткие правила уже изначально имеют наглядный смысл. Например,

Конечно заманчиво иметь возможность получения не только качественного, но и количественного правила, связывающего уровень разрыва в доходах с преступностью. Мы знаем, что нейронные сети типа персептрона являются универсальными аппроксиматорами и могут реализовать любое количественное отображение. Хорошо бы поэтому построить нейронную сеть так, чтобы она, во-первых, воспроизводила указанное нечеткое качественное правило (чтобы изначально знать интерпретацию работы сети) и, во-вторых, давала хорошие количественные предсказания для соответствующего параметра (уровня преступности). Очевидно, что добиться этого можно подбором соответствующих функций принадлежности. А именно, задача состоит в том, чтобы так определить понятия "высокий разрыв в доходах" и "повышенный уровень преступности", чтобы выполнялись и качественные и количественные соотношения. Нужно, чтобы и сами эти определения не оказалось дикими - иначе придется усомниться в используемом нами нечетком правиле. Если такая задача успешно решается, то это означает успешный симбиоз теории нечетких множеств и нейронных сетей, в которых "играют" наглядность первых и универсальность последних.
Заметим, что использованные нами ранее функции принадлежности носили достаточно специфический характер (так называемую треугольную форму). Успех же сочетания нечетких моделей существенно зависит от разумного нечеткого разбиения пространств входов и выходов. Вследствие этого, задача адаптации функций принадлежности может быть поставлена как задача оптимизации, для решения которой и могут использоваться нейронные сети.
Наиболее простой путь для этого заключается в выборе некоторого вида функции принадлежности, форма которой управляется рядом параметров, точное значение которых находится при обучении нейронной сети.
Рассмотрим соответствующую методику на следующем примере.Обозначим






Формально, эти правила можно записать следующим образом


























Для нечетких оценок величины портфеля вводятся следующие функции принадлежности





Предположим, что точные количественные значения курса доллара по отношению к немецкой марке, шведской кроне и финской марке равны




Теперь можно вычислить и количественные оценки величины портфеля, даваемые каждым из наших правил,



Оценка величины портфеля получается усреднением вышеприведенных оценок по уровням активации каждого из правил

Ниже на рисунке приведена архитектура нейронной сети, эквивалентной описанной выше нечеткой системе ( рисунок 11.4).

Рис. 11.4. Нейронная сеть (нечеткий персептрон), входами которой являются лингвистические переменные, выходом - четкое значение величины портфеля.
Скрытые слои в нечетком персептроне называются слоями правил
Значения выходов в узлах первого слоя отражают степень соответствия входных значений лингвистическим переменным, связанными с этими узлами. Элементы второго слоя вычисляют значения уровней активации соответствующих нечетких правил. Выходные значения нейронов третьего слоя соответствуют нормированным значениям этих уровней активации

Выходные значения нейронов четвертого слоя вычисляются как произведения нормированных значений уровней активации правил на значения величины портфеля, соответствующего данной их (ненормированной)активации.

Наконец, единственный выходной нейрон (слой 5) просто суммирует воздействия нейронов предыдущего слоя.
Если мы имеем набор обучающих пар, содержащих точные значения курсов обмена








Аналогичным образом выводятся уравнения коррекции для параметров, управляющих формой функций принадлежности нечетких понятий слабый



Что лучше, статистические методы или нейронные сети?
Лучшим ответом на этот сугубо практический для прикладника вопрос является "It depends". По-русски это означает "Все зависит от ситуации". Иногда, особенно если априорная информация о данных отсутствует, разумнее использовать нейронные сети. Такой выбор часто дает быстрое и качественное решение задачи, как правило не худшее, чем получаемое статистическими методами после тщательного изучения структуры данных.
Иногда высказывается такое мнение, что статистические методы предназначены для профессионалов, поскольку их использование требует основательной теоретической подготовки. В то же время, нейронные сети - это инструмент любителей, который можно быстро освоить и применять. Как бы то ни было, разработка нейросетевой системы анализа данных действительно может быть осуществлена за значительно более короткое время (порядка нескольких месяцев) нежели создание аналогичной системы статистического анализа (требующее годы). Например, бизнес-стратег Дэниэл Баррас, автор "Technotrands: How to Use Technology to Go Beyond Your Competition" утверждает, что для того, чтобы остаться конкурентноспособным, деловой человек должен не только использовать инструменты будущего, но и использовать их по-новому. В частности, нейросетевые технологии снабжают людей экспертизой, которая прежде могла быть получена лишь в течении многих лет обучения и опыта.
При наличии дополнительных знаний о характере задачи статистические данные могут оказаться предпочтительнее. При сравнительном анализе возможностей нейронных сетей и статистических методов надо быть достаточно осторожными, поскольку иногда весьма сложные нейросетевые подходы сопоставляются с простыми статистическими моделями или наоборот. Существует мнение, что одинаково мощные статистические и нейросетевые подходы дают результаты одинаковые по точности и по затратам. Тем не менее, примеры решения действительно важных прикладных задач могут дать представление о возможностях того или иного подхода.
Очень важной является проблема диагностирования инфаркта миокарда в приемном покое.
Опытные врачи правильно определяют это заболевание в 88% случаев и в 29% случаев дают ложную тревогу. Разнообразные статистические методы, включая дискриминантный анализ, логистическую регрессию, рекурсивный анализ распределений и пр. смогли лишь незначительно снизить число ложных тревог (до 26%). А вот Вильям Бакст, работающий на медицинском факультете университета в Сан-Диего, использовал для диагностики многослойный персептрон и повысил число правильно диагностированных инфарктов до 92%. Но более впечатляющим его результатом было снижение числа ложных тревог до 4%(!). Заметим, что такое значительное уменьшение ложно-положительных реакций является достаточно типичным преимуществом использования нейронных сетей. Эта особенность стимулирует в настоящее время разработку нейросетевых систем диагностики рака молочной железы, для которой ложные диагнозы являются настоящим бичом.
Дэвид Эшби и Нед Кумар из Школы Бизнеса в Арканзасе сравнили результаты применения нейросетевой технологии и классического дискриминантного анализа к предсказанию невыполнения обязательств по высокодоходным облигациям ("junk-bonds"). Такие облигации являются в настоящее время основным источником внешнего финансирования американских корпораций. Невыполнение обязательств означает либо потерю интереса к компании, либо потерю финансирования. Поскольку операции с такими облигациями носят ярко выраженный спекулятивный характер, то предсказание выхода их из игры представляет интерес для ее участников. Задача состоит в классификации облигаций на два класса: выполнят - не выполнят. Первичный набор признаков, характеризовавших каждую облигацию, включал 29 финансовых и рыночных показатели фирм, из которых после корреляционного анализа было отобрано 16. Линейный дискриминантный анализ позволил провести классификацию с точностью 87.5%, в то время как двухслойный персептрон (16 нейронов в скрытом слое) дал несколько лучший результат - 89.3% правильных ответов.
Нейронные сети помогают выявить связи между данными в тех случаях, когда статистические методы не справляются с задачей.Например, статистика не позволяет найти корреляцию в последовательностях ДНК двух бактериофагов PHIX174 и MIG4XX, хотя было известно, что они являются ближайшими родственниками. Использование сетей Хопфилда для поиска в этих последовательностях скрытых повторов (периодичностей), обеспечившее учет корреляций между нуклеотидными парами, не только показало несомненную близость геномов этих фагов, но и продемонстрировало, что они представляют собой гены, "сбежавшие" с комплементарных цепей ДНК-предшестенницы.
Фазовые переходы
На простом примере можно убедиться, что свойства сети критическим образом зависят от температуры



Решение этого уравнения зависит от крутизны наклона функции гиперболического тангенса в начале координат (см. рисунок 11.5). При высокой температуре




Рис. 11.5. Иллюстрация к характеру решений уравнения среднего поля в приближении высокой и низкой температур
Однако, при снижении температуры ниже точки Кюри


Такое поведение характерно и для общего случая. Мы увидим далее, что в модели Хопфилда свойства ассоциативного запоминания и вызова образов проявляются в некоторой области температуры и дополнительного параметра - степени загрузки памяти. Вне этой области система переходит в неупорядоченное состояние.
Извлечение правил if-then
В лекции, посвященной извлечению знаний, мы уже познакомились с нейросетевыми методами извлечения правил из данных. Настало время узнать, как можно извлечь с их помощью нечеткие правила.
Рассмотрим набор нечетких правил

Если





Каждое из них может интерпретироваться как обучающая пара для многослойного персептрона. При этом, условие (x есть




Если же правила имеют более сложный вид, типа "два входа - один выход":

Если







В методе Умано и Изавы нечеткое множество представляется конечным числом значений совместимости. Пусть








Дискретный аналог обучающего множества правил (заменяющее функциональное) имеет вид:

Если теперь ввести обозначения



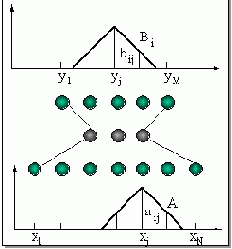
Рис. 11.3. Нечеткая нейронная сеть и треугольные функции принадлежности входных и выходных переменных
Пример 1. Предположим, что обучающая выборка включает три правила:



Функции принадлежности определим как






(Здесь предполагается, что доход не превышает 100% или 1.0 в относительных величинах)
Тогда обучающая выборка принимает форму {(малый, отрицательный), (средний, близок к нулю), (большой, положительный)}
Если носитель множества входов [0, 10 000 000], то для покрытия множества населения городов равномерной сеткой, захватывающей и малые города, понадобится несколько сот точек. Поэтому, ограничимся городами с населением 1 000 000 человек. Тогда можно выбрать


В методе Уехары и Фуджицы вместо разбиения равномерной сеткой области, покрывающей носители всех функций принадлежности, равномерно разбивается область изменения этих функций [0,1]. Здесь видна явная аналогия с переходом от интегрирования по Риману к интегралу Лебега. Остальные действия аналогичны уже описанным.
Являются ли нейронные сети языком описания?
Как уже отмечалось, некоторые статистики утверждают, что нейросетевые подходы к обработке данных являются просто заново переоткрытыми и переформулированными, но хорошо известными статистическими методами анализа. Иными словами, нейрокомпьютинг просто пользуется новым языком для описания старого знания. В качестве примера приведем цитату из Уоррена Сэрла:
Многие исследователи нейронных сетей являются инженерами, физиками, нейрофизиологами, психологами или специалистами по компьютерам, которые мало знают о статистике и нелинейной оптимизации. Исследователи нейронных сетей постоянно переоткрывают методы, которые известны в математической и статистической литературе десятилетиями и столетиями, но часто оказываются неспособными понять как работают эти методы
Подобная точка зрения, на первый взгляд, может показаться обоснованной. Формализм нейронных сетей действительно способен претендовать на роль универсального языка. Не случайно уже в пионерской работе МакКаллока и Питтса было показано, что нейросетевое описание эквивалентно описанию логики высказываний.
Я в действительности обнаружил, что с помощью с помощью техники, которую я разработал в работе1961 года (…), я мог бы легко ответить на все вопросы, которые мне задают специалисты по мозгу (...) или компьютерщики. Как физик, однако, я хорошо знал, что теория, которая объясняет все, на самом деле не объясняет ничего: в лучшем случае она является языком. Эдуардо Каянелло
Не удивительно поэтому, что статистики часто обнаруживают, что привычные им понятия имеют свои аналоги в теории нейронных сетей. Уоррен Сэрл составил небольшой словарик терминов, использующихся в этих двух областях.
| Признаки | переменные |
| входы | независимые переменные |
| выходы | предсказанные значения |
| целевые значения | зависимые переменные |
| ошибка | невязка |
| обучение, адаптация, самоорганизация | оценка |
| функция ошибки, функция Ляпунова | критерий оценки |
| обучающие образы (пары) | наблюдения |
| параметры сети: веса, пороги. | Оценочные параметры |
| нейроны высокого порядка | взаимодействия |
| функциональные связи | трансформации |
| обучение с учителем или гетероассоциация | регрессия и дискриминантный анализ |
| обучение без учителя или автоассоциация | сжатие данных |
| соревновательное обучение, адаптивная векторная квантизация | кластерный анализ |
| обобщение | интерполяция и экстраполяция |
Элементы нечеткой логики
Центральным понятием нечеткой логики является понятие лингвистической переменной. Согласно Лотфи Заде лингвистической называется переменная, значениями которой являются слова или предложения естественного или искусственного языка. Примером лингвистической переменной является, например, падение производства, если она принимает не числовые, а лингвистические значения, такие как, например, незначительное, заметное, существенное, и катастрофическое. Очевидно, что лингвистические значения нечетко характеризуют имеющуюся ситуацию. Например, падение производства на 3% можно рассматривать и как в какой-то мере незначительное, и как в какой-то мере заметное. Интуитивно ясно, что мера того, что данное падение является катастрофическим должна быть весьма мала.
Смысл лингвистического значения X и характеризуется выбранной мерой - так называемой функций принадлежности (membership function)

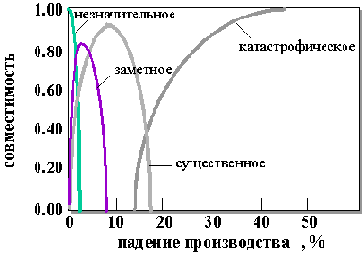
Рис. 11.2. Функции принадлежности лингвистической переменной Падение производства
Нечеткое правило связывает значения лингвистических переменных. Примером такого правила может быть, например, следующее.
Если (падение производства - катастрофическое), то (доходы от экспорта энергоресурсов - значительные).
Нечеткое подмножество универсального множества U характеризуется функцией принадлежности



Носителем множества A называется множество таких точек в U, для которых величина

Нечеткие нейроны
Преобразование, осуществляемое типичным нейроном с двумя входами, имеет вид


Если осуществить соответствующие замены в преобразовании, осуществляемом знакомым нам нейроном, и положить в нем


Для нечетких нейронов полагается, что значения входов и весов заключены в интервале [0, 1], поэтому и выход нейрона ИЛИ будет принадлежать этому же интервалу.
Используя противоположную подстановку (умножение max), (сложение min ) получим преобразование, характерное для нечеткого И-нейрона:

Нейронные сети и экспертные системы
Рассмотрим теперь отношения нейрокомпьютинга и экспертных систем. Обе эти технологии иногда относят к направлению Искусственный Интеллект, хотя строго говоря, термин искусственный интеллект появился в 70-е годы в связи с экспертными системами, как направления альтернативного нейронным сетям.
Первая конференция по проблемам искусственного интеллекта состоялась в США в 1969 году - в этом же году и была опубликована критическая книга Минского и Пейперта "Персептроны".
Его основатели - Марвин Минский и Эдвард Фейгенбаум посчитали излишней апелляцию к архитектуре мозга, его нейронным структурам, и декларировали необходимость моделирования работы человека со знаниями. Тем самым, поставив в центр внимания операции с формально-логическими языковыми структурами, они заведомо выбрали ориентацию на имитацию обработки информации левым полушарием мозга человека. Системы обработки таких формализованных знаний были названы экспертными, поскольку они должны были воспроизводить ход логических рассуждений эксперта (высокопрофессионального специалиста) в конкретной предметной области. Эти рассуждения проводятся с использованием правил вывода, которые инженер знаний должен извлечь у эксперта.
Заметим, что в настоящее время распространено более широкое толкование систем искусственного интеллекта. К ним относят не только экспертные , но и нечеткие системы, нейронные сети и всевозможные комбинации, такие как нечеткие экспертные системы или нечеткие нейронные системы. Отдельным направлениями, выделяются также эвристический поиск, в рамках которого в 80-е годы Ньюэллом и Саймоном был разработан Общий Решатель Задач (GPS - General Problem Solver), а также обучающиеся машины (Ленат, Холланд). И если GPS не мог решать практические задачи, то машинная обучающаяся система EURISCO внесла значительный вклад в создание СБИС, изобретя трехмерный узел типа И/ИЛИ.
Однако, экспертные системы претендовали именно на решение важных прикладных задач прежде всего в таких областях, как медицина и геология.
При этом соответствующая технология в сочетании с нечеткими системами была в 1978 году положена японцами в основу программы создания компьютеров 5-го поколения.
Парадокс искусственного интеллекта заключается в том, что как только некоторая, кажущаяся интеллектуальной, деятельность оказывается искусственно реализованной, она перестает считаться интеллектуальной. В этом смысле наибольшие шансы остаться интелелктуальными имеют как раз нейронные сети, из которых еще не извлечены артикулированные знания.
Сопоставление экспертных систем и нейрокомпьютинга выявляет различия, многие из которых характерны для уже отмечавшихся в первой лекции различий обычных компьютеров (а экспертные системы реализуются именно на традиционных машинах, главным образом на языке ЛИСП и Пролог) и нейрокомпьютеров
Аналогия | правое полушарие | левое полушарие |
Объект | данные | знания |
Вывод | отображение сетью | правила вывода |
Важным преимуществом нейронных сетей является то, что разработка экспертных систем, основанных на правилах требует 12-18 месяцев, а нейросетевых - от нескольких недель до месяцев.
Рассматривая извлечение знаний из обученных нейронных сетей мы уже показали, что представление о них, как о черных ящиках, не способных объяснить полученное решение (это представление иногда рассматривается как аргумент в пользу преимущества экспертных систем перед нейросетями), неверно. В то же время, очевидно, что как и в случае мозга, в котором левое и правое полушарие действуют сообща, естественно и объединение экспертных систем с искусственными нейронными сетями. Подобные синтетические системы могут быть названы нейронными экспертными системами - этот термин использовал Иржи Шима, указавший на необходимость интеграции достоинств обоих типов систем. Такая интеграция может осуществляться двояким образом. Если известна только часть правил, то можно либо инициализировать веса нейронной сети исходя из явных правил, либо инкорпорировать правила в уже обученные нейронные сети.Шима предложил использовать и чисто коннекционистский методику построения нейронных эксперных систем, которая обладает такимдостоинством, как возможность работы с неполными данными (ситуация типичная для реальных баз данных). Такой возможностью обладают введенные им сети интервальных нейронов.
Нейронные сети и нечеткая логика
Системы нечеткой логики (fuzzy logics systems) могут оперировать с неточной качественной информацией и объяснять принятые решения, но не способны автоматически усваивать правила их вывода. Вследствие этого, весьма желательна их кооперация с другими системами обработки информации для преодоления этого недостатка. Подобные системы сейчас активно используются в различных областях, таких как контроль технологических процессов, конструирование, финансовые операции, оценка кредитоспособности, медицинская диагностика и др. Нейронные сети используются здесь для настройки функций принадлежности нечетких систем принятия решений. Такая их способность особенно важна при решении экономических и финансовых задач, поскольку вследствие их динамической природы функции принадлежности неизбежно должны адаптироваться к изменяющимся условиям.
Хотя нечеткая логика может явно использоваться для представления знаний эксперта с помощью правил для лингвистических переменных, обычно требуется очень много времени для конструирования и настройки функций принадлежности, которые количественно определяют эти переменные. Нейросетевые методы обучения автоматизируют этот процесс и существенно сокращают время разработки и затраты на нее, улучшая при этом параметры системы. Системы, использующие нейронные сети для определения параметров нечетких моделей, называются нейронными нечеткими системами. Важнейшим свойством этих систем является их интерпретируемость в терминах нечетких правил if-then.
Подобные системы именуются также кооперативными нейронными нечеткими системами и противопоставляются конкурентным нейронным нечетким системам, в которых нейронные сети и нечеткие системы работают вместе над решением одной и той же задачи, не взаимодействуя друг с другом. При этом нейронная сеть обычно используется для предобработки входов или же для постобработки выходов нечеткой системы.
Кроме них имеются также нечеткие нейронные системы. Так называются нейронные сети, использующие методы нечеткости для ускорения обучения и улучшения своих характеристик.
Это может достигаться, например, использованием нечетких правил для изменения темпа обучения или же рассмотрением нейронных сетей с нечеткими значениями входов.
Существует два основных подхода к управлению темпом обучения персептрона методом обратного распространения ошибки. При первом этот темп одновременно и равномерно уменьшается для всех нейронов сети в зависимости от одного глобального критерия - достигнутой среднеквадратичной погрешности на выходном слое. При этом сеть быстро учится на начальном этапе обучения и избегает осцилляций ошибки на позднем. Во втором случае оцениваются изменения отдельных межнейронных связей. Если на двух последующих шагах обучения инкременты связей имеют противоположный знак, то разумно уменьшить соответствующий локальный темп - впротивном случае его следует увеличить. Использование нечетких правил может обеспечить более аккуратное управление локальными темпами модификации связей. В чаcтности это может быть достигнуто, если в качестве входных параметров этих правил использовать последовательные значения градиентов ошибки. Таблица соответствующих правил может иметь, например следующий вид:
| NB | NS | Z | PS | PB | |
| NB | PB | PS | Z | NS | NB |
| NS | NS | PS | Z | NS | NB |
| Z | NB | NS | Z | NS | NB |
| PS | NB | NS | Z | PS | NS |
| PB | NB | NS | Z | PS | PB |
Лингвистические переменные Темп Обучения и Градиент принимают в иллюстрируемом таблицей нечетком правиле адаптации следующие значения: NB - большой отрицательный; NS - малый отрицательный; Z - близок к нулю; PS - малый положительный; PB - большой положительный.
Наконец, в современных гибридных нейронных нечетких системах нейронные сети и нечеткие модели комбинируются в единую гомогенную архитектуру. Такие системы могут интерпретироваться либо как нейронные сети с нечеткими параметрами, либо как параллельные распределенные нечеткие системы.
Нейронные сети и статистическая физика
Данная тема заслуживает не одной книги и ей действительно посвящена обширнейшая литература. В настоящем курсе лекций мы не можем хоть сколько-нибудь подробно остановится на ней. Рассмотрим кратко лишь применение соответствующих идей к анализу сети Хопфилда. Демонстрация тесной аналогии, существующей между спиновыми стеклами и нейронными сетями, определила массированное и плодотворное вторжение методов статистической физики в теорию нейронных сетей в начале восьмидесятых годов. Сеть Хопфилда со стохастическими нейронами и явилась главной моделью, в которой применение этих методов оказалось наиболее значительным. Это чрезвычайно плодотворное обобщение модели, в некотором смысле эквивалентное переходу к сетям с градуальными нейронами. В нем нейроны являются стохастическими элементами и это обстоятельство открывает путь использованию методов статистической физики для анализа свойств ассоциативной памяти.
Нейронные сети и статистика
Поскольку в настоящее время нейронные сети с успехом используются для анализа данных, уместно сопоставить их со старыми хорошо разработанными статистическими методами. В литературе по статистике иногда можно встретить утверждение, что наиболее часто применяемые нейросетевые подходы являются ни чем иным, как неэффективными регрессионными и дискриминантными моделями. Мы уже отмечали прежде, что многослойные нейронные сети действительно могут решать задачи типа регрессии и классификации. Однако, во-первых, обработка данных нейронными сетями носит значительно более многообразный характер - вспомним, например, активную классификацию сетями Хопфилда или карты признаков Кохонена, не имеющие статистических аналогов. Во-вторых, многие исследования, касающиеся применения нейросетей в финансах и бизнесе, выявили их преимущества перед ранее разработанными статистическими методами. Рассмотрим подробнее результаты сравнения методов нейросетей и математической статистики.
Перекрестное опыление.
Конструктивный взгляд на взаимоотношение нейронных сетей и статистических методов заключается в том, что в общем случае они должны помогать друг другу и обогащать друг друга. Кристоф и Пьер Кувре назвали такой процесс перекрестным опылением.
Например, было показано, что нейросетевые классификаторы оценивают апостериорную Байесовскую вероятность и поэтому аппроксимируют оптимальный статистический классификатор с минимальной ошибкой. Подобная статистическая интерпретация значений выходов нейронной сети позволяет, в частности, компенсировать обычно существующие диспропорции в объемах примеров, представляющих в обучающей выборке различные классы.
Почему статистики ревнуют специалистов по нейронным сетям, а не наоборот?
Среди так или иначе конкурирующих методологий (а нейронные сети и статистика имеют общую часть "электората" - анализ данных) как правило побеждает не более обоснованная и надежная, а та, что ставит новые задачи для исследования (Имре Лакатош). Нейрокомпьютинг гораздо более молодая отрасль знания нежели статистика. Он бросает многочисленные вызовы специалистам различных профессий: биологам, физикам, психологам, математикам и другим. Кроме того, сфера теории нейронных сетей гораздо шире анализа данных. Она включает в себя и моделирование мозга и разработку нейрокомпьютеров. Статистики не могут претендовать на соревнование в этих областях и ревностно следят за претензиями нейрокомпьютинга на их экологическую нишу.
Практические выводы
Джон Такер провел тщательное сравнительное исследование использования логистической регрессии и нейронных сетей и определил следующее их принципиальное различие, которое сохраняет свое значение и при общем сопоставления статистики и нейрокомпьютинга. В то время как статистические методы фокусируются на оптимальном методе выбора переменных, нейрокомпьютинг ставит во главу угла предобработку этих переменных. Если нейронная сеть представляет собой многослойный персептрон, то функцией скрытых слоев и является такая последовательная предобработка данных. Вследствие этого нейронные сети занимают уникальное место среди методов обработки данных, превосходя их в универсальности и сложности, оставаясь при этом data-driven методом мало чувствительным к форме данных как таковых.
Главный практический вывод, который может сделать читатель, сводится к фразе, уже ставшей афоризмом:
Если ничего не помогает, попробуйте нейронные сети.
Приближение среднего поля
Поскольку динамика состояний стохастических нейронов является вероятностной, можно интересоваться только средней активностью, или же ожидаемыми значениями их состояний

В силу нелинейности функции Ферми усреднение ее затруднительно, но в приближении среднего поля


Сеть Хопфилда с Хеббовскими связями
Рассмотрим интересующий нас случай сети, в которой связи вычислены по Хеббовскому правилу, исходя из вида запоминаемых векторов. В этом случае уравнения среднего поля принимают вид

Если сеть работает как ассоциативная память, то разумно предположить, что каждому запоминаемому вектору


Подставляя это выражение в уравнения среднего поля и используя предположение, что все векторы памяти не коррелированы и значения их компонент с равной вероятностью принимают значения , получим:

В пределе



Вновь при высокой температуре








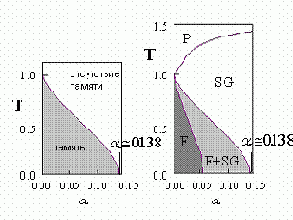
Рис. 11.6. Упрощенная и детальная диаграммы фазовых состояний сети Хопфилда
Наличие тепловых флуктуаций снижает вероятность попадания сети в состояние ложных минимумов. Критическая температура, при которых множество таких минимумов становится неустойчивыми, равна


Сети интервальных нейронов
Ситуация, в которой некоторые данные не известны или не точны, встречается достаточно часто. Например, при оценке возможностей той или иной фирмы, можно учитывать ее официально декларируемый капитал, скажем в 100 миллионов, но лучше всего считать, что в действительности его величина является несколько большей и меняется в интервале от 100 до 300 млн. Удобно ввести в данном случае специальные нейроны, состояния которых кодируют не бинарные или непрерывные значения, а интервалы значений. В случае, если нижняя и верхняя граница интервала совпадают, то состояния таких нейронов становятся аналогичными состояниям обычных нейронов.
Для интервального нейрона









Интервальное значение, которое принимает


где

Передаточная функция интервального нейрона приблизительно отражает идею монотонности по отношению к операции интервального включения. Это означает, что при





Стохастические нейроны
Стохастический нейрон, как и в оригинальной модели Хопфилда, является бинарным - его состояние







где




В чем различие нейронных сетей и статистики?
В чем же заключается сходство и различие языков нейрокомпьютинга и статистики в анализе данных. Рассмотрим простейший пример.
Предположим, что мы провели наблюдения и экспериментально измерили N пар точек, представляющих функциональную зависимость






Если параметры


Та же самая задача может быть решена с использованием однослойной сети с единственным входным и единственным линейным выходным нейроном. Вес связи a и порог b могут быть получены путем минимизации той же величины невязки (которая в данном случае будет называться среднеквадратичной ошибкой) в ходе обучения сети, например методом backpropagation. Свойство нейронной сети к обобщению будет при этом использоваться для предсказания выходной величины по значению входа.
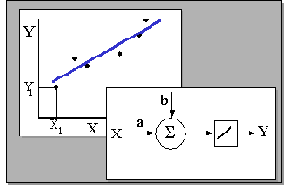
Рис. 11.1. Линейная регрессия и реализующий ее однослойный персептрон
При сравнении этих двух подходов сразу бросается в глаза то, что при описании своих методов статистика апеллирует к формулам и уравнениям, а нейрокомпьютинг к графическому описанию нейронных архитектур.
Если вспомнить, что с формулами и уравнениями оперирует левое полушарие, а с графическими образами правое, то можно понять, что в сопоставлении со статистикой вновь проявляется "правополушарность" нейросетевого подхода.
Еще одним существенным различием является то, что для методов статистики не имеет значения, каким образом будет минимизироваться невязка - в любом случае модель остается той же самой, в то время как для нейрокомпьютинга главную роль играет именно метод обучения.
В чем же заключается сходство и различие языков нейрокомпьютинга и статистики в анализе данных. Рассмотрим простейший пример.
Предположим, что мы провели наблюдения и экспериментально измерили N пар точек, представляющих функциональную зависимость






Если параметры


Та же самая задача может быть решена с использованием однослойной сети с единственным входным и единственным линейным выходным нейроном. Вес связи a и порог b могут быть получены путем минимизации той же величины невязки (которая в данном случае будет называться среднеквадратичной ошибкой) в ходе обучения сети, например методом backpropagation. Свойство нейронной сети к обобщению будет при этом использоваться для предсказания выходной величины по значению входа.

Рис. 11.1. Линейная регрессия и реализующий ее однослойный персептрон
При сравнении этих двух подходов сразу бросается в глаза то, что при описании своих методов статистика апеллирует к формулам и уравнениям, а нейрокомпьютинг к графическому описанию нейронных архитектур.
Если вспомнить, что с формулами и уравнениями оперирует левое полушарие, а с графическими образами правое, то можно понять, что в сопоставлении со статистикой вновь проявляется "правополушарность" нейросетевого подхода.
Еще одним существенным различием является то, что для методов статистики не имеет значения, каким образом будет минимизироваться невязка - в любом случае модель остается той же самой, в то время как для нейрокомпьютинга главную роль играет именно метод обучения.
Иными словами, в отличие от нейросетевого подхода, оценка параметров модели для статистических методов не зависит от метода минимизации. В то же время статистики будут рассматривать изменения вида невязки, скажем на

как фундаментальное изменение модели.
В отличие от нейросетевого подхода, в котором основное время забирает обучение сетей, при статистическом подходе это время тратится на тщательный анализ задачи. При этом опыт статистиков используется для выбора модели на основе анализа данных и информации, специфичной для данной области. Использование нейронных сетей - этих универсальных аппроксиматоров - обычно проводится без использования априорных знаний, хотя в ряде случаев оно весьма полезно. Например, для рассматриваемой линейной модели использование именно среднеквадратичной ошибки ведет к получению оптимальной оценки ее параметров, когда величина шума имеет нормальное распределение с одинаковой дисперсией для всех обучающих пар. В то же время если известно, что эти дисперсии различны, то использование взвешенной функции ошибки

может дать значительно лучшие значения параметров.
Помимо рассмотренной простейшей модели можно привести примеры других в некотором смысле эквивалентных моделей статистики и нейросетевых парадигм
| Многослойный персептрон | Нелинейная (в т.ч. логистическая) регрессия, Дискриминантные модели |
| Автоассоциативный персептрон | Анализ главных компонент |
| Векторная квантизация | Кластеризация с k-средними |
| Сети нейронов высоких порядков | Полиномиальная регрессия |
Сеть Хопфилда имеет очевидную связь с кластеризацией данных и их факторным анализом.
Факторный анализ используется для изучения структуры данных. Основной его посылкой является предположение о существовании таких признаков - факторов, которые невозможно наблюдать непосредственно, но можно оценить по нескольким наблюдаемым первичным признакам. Так, например, такие признаки, как объем производства и стоимость основных фондов, могут определять такой фактор, как масштаб производства.
В отличие от нейронных сетей, требующих обучения, факторный анализ может работать лишь с определенным числом наблюдений. Хотя в принципе число таких наблюдений должно лишь на единицу превосходить число переменных рекомендуется использовать хотя бы втрое большее число значение. Это все равно считается меньшим, чем объем обучающей выборки для нейронной сети. Поэтому статистики указывают на преимущество факторного анализа, заключающееся в использовании меньшего числа данных и, следовательно, приводящего к более быстрой генерации модели. Кроме того, это означает, что реализация методов факторного анализа требует менее мощных вычислительных средств. Другим преимуществом факторного анализа считается то, что он является методом типа white-box, т.е. полностью открыт и понятен - пользователь может легко осознавать, почему модель дает тот или иной результат. Связь факторного анализа с моделью Хопфилда можно увидеть, вспомнив векторы минимального базиса для набора наблюдений (образов памяти - см. Лекцию 5). Именно эти векторы являются аналогами факторов, объединяющих различные компоненты векторов памяти - первичные признаки.
Иными словами, в отличие от нейросетевого подхода, оценка параметров модели для статистических методов не зависит от метода минимизации. В то же время статистики будут рассматривать изменения вида невязки, скажем на

как фундаментальное изменение модели.
В отличие от нейросетевого подхода, в котором основное время забирает обучение сетей, при статистическом подходе это время тратится на тщательный анализ задачи. При этом опыт статистиков используется для выбора модели на основе анализа данных и информации, специфичной для данной области. Использование нейронных сетей - этих универсальных аппроксиматоров - обычно проводится без использования априорных знаний, хотя в ряде случаев оно весьма полезно. Например, для рассматриваемой линейной модели использование именно среднеквадратичной ошибки ведет к получению оптимальной оценки ее параметров, когда величина шума имеет нормальное распределение с одинаковой дисперсией для всех обучающих пар. В то же время если известно, что эти дисперсии различны, то использование взвешенной функции ошибки

может дать значительно лучшие значения параметров.
Помимо рассмотренной простейшей модели можно привести примеры других в некотором смысле эквивалентных моделей статистики и нейросетевых парадигм
| Многослойный персептрон | Нелинейная (в т.ч. логистическая) регрессия, Дискриминантные модели |
| Автоассоциативный персептрон | Анализ главных компонент |
| Векторная квантизация | Кластеризация с k-средними |
| Сети нейронов высоких порядков | Полиномиальная регрессия |
Сеть Хопфилда имеет очевидную связь с кластеризацией данных и их факторным анализом.
Факторный анализ используется для изучения структуры данных. Основной его посылкой является предположение о существовании таких признаков - факторов, которые невозможно наблюдать непосредственно, но можно оценить по нескольким наблюдаемым первичным признакам. Так, например, такие признаки, как объем производства и стоимость основных фондов, могут определять такой фактор, как масштаб производства.
В отличие от нейронных сетей, требующих обучения, факторный анализ может работать лишь с определенным числом наблюдений. Хотя в принципе число таких наблюдений должно лишь на единицу превосходить число переменных рекомендуется использовать хотя бы втрое большее число значение. Это все равно считается меньшим, чем объем обучающей выборки для нейронной сети. Поэтому статистики указывают на преимущество факторного анализа, заключающееся в использовании меньшего числа данных и, следовательно, приводящего к более быстрой генерации модели. Кроме того, это означает, что реализация методов факторного анализа требует менее мощных вычислительных средств. Другим преимуществом факторного анализа считается то, что он является методом типа white-box, т.е. полностью открыт и понятен - пользователь может легко осознавать, почему модель дает тот или иной результат. Связь факторного анализа с моделью Хопфилда можно увидеть, вспомнив векторы минимального базиса для набора наблюдений (образов памяти - см. Лекцию 5). Именно эти векторы являются аналогами факторов, объединяющих различные компоненты векторов памяти - первичные признаки.
Логистическая регрессия является методом бинарной классификации, широко применяемом при принятии решений в финансовой сфере. Она позволяет оценивать вероятность реализации (или нереализации) некоторого события в зависимости от значений некоторых независимых переменных - предикторов:



Достоинством нейронных сетей является то, что такая ситуация не представляет для них проблемы. Кроме того, нейросети нечувствительны к корреляции значений предикторов, в то время как методы оценки параметров регрессионной модели в этом случае часто дают неточные значения. В то же время многие нейронные парадигмы, такие как сети Кохонена или машина Больцмана не имеют прямых аналогов среди статистических методов.
В каком-то смысле недоверие и даже "ревность" к нейросетевым методам в сообществе статистиков аналогичны такому же отношению, существовавшему в недалеком прошлом среди специалистов в области Искусственного Интеллекта. Теперь же значительную часть публикаций в журналах типа Artificial Intelligence (AI) или AI Expert составляют работы, посвященные нейронным технологиям. В настоящее время в статистическом сообществе растет интерес к нейронным сетям, как с теоретической, так и с практической точек зрения. Это проявляется в инкорпорации нейросетевых средств в стандартные статистические пакеты, такие как SAS и SPSS.

