Кубические модели нейронов
Вектор


вектора

существует

Можно рассматривать ячейки памяти, как вершины


Двоичный вход



через


Модель нейрона Хебба
Структурная схема нейрона Хебба соответствует стандартной форме модели нейрона (рис.1). Д.Хебб предложил формальное правило, в котором вес


где

При обучении с учителем вместо выходного сигнала



В каждом цикле обучения происходит суммирование текущего значения веса и его приращения


В результате применения правила Хебба веса нейрона могут принимать произвольно большие значения. Один из способов стабилизации процесса обучения по правилу Хебба состоит в учете последнего значения



Значение



Нейрон с квадратичным сумматором
Квадратичный сумматор может вычислять произвольный полином второго порядка от вектора входных сигналов

Для многомерных нормальных распределений нейрон с квадратичным сумматором является наилучшим классификатором. Минимум вероятности ошибки дает квадратичная разделяющая поверхность:
если

если

Квадратичная ошибка здесь определяется как

Коэффициенты квадратичного сумматора уточняются по формулам

Недостаток такого классификатора - большое число настраиваемых параметров.
Нейрон типа "адалайн"
В нейроне типа "адалайн" (ADAptive LInear Neuron - адаптивный линейный нейрон) адаптивный подбор весовых коэффициентов осуществляется в процессе минимизации квадратичной ошибки, определяемой как

В связи с выполнением условия дифференцируемости целевой функции стало возможным применение алгоритма градиентного обучения. Значения весовых коэффициентов уточняются следующим способом

Нейроны типа WTA
Нейроны типа WTA (Winner Takes All — "Победитель получает все") имеют входной модуль в виде адаптивного сумматора. Выходной сигнал


По результатам сравнения сигналов

отдельных нейронов победителем признается нейрон, у которого

Для обучения нейронов WTA учитель не требуется. На начальном этапе случайным образом выбираются весовые коэффициенты


После подачи входного вектора


определяется победитель этапа. Победитель переходит в состояние 1, что позволяет произвести уточнение весов его входных линий


Проигравшие нейроны формируют на своих выходах состояние 0, что блокирует процесс уточнения их весовых коэффициентов.
Выходной сигнал


Поскольку


определяется углом между векторами




Следствием конкуренции нейронов становится самоорганизация процесса обучения. Нейроны уточняют свои веса таким образом, что при предъявлении группы близких по значениям входных векторов победителем всегда оказывается один и тот же нейрон. Системы такого типа чаще всего применяются для классификации векторов.
Обучение кубических нейронов
Кубические нейроны обучаются путем изменения содержимого ячейки их памяти. Обозначим через `+' операцию инкремента-установки содержимого ячейки в +1, через `-' операцию декремента-установки в -1.
Пусть в начальном состоянии все ячейки кубического нейрона установлены в ноль. Обозначим ячейки, адресуемые обучающей выборкой, как центральные ячейки или центры. Ячейки, близкие к центрам в смысле расстояния Хемминга, будем настраивать на те же или близкие к ним значения, что и сами центры, т.е. должна происходить кластеризация значений ячейки вокруг центра. Это условие должно выполнятся для сети из кубических нейронов. Алгоритм обучения строит так называемое разбиение Вороного, при котором значение в ячейке определяется значением в ближайшем центре, а ячейки, равноудаленные от центров, остаются установленными в ноль. Кубические нейроны допускают большую функциональность, чем полулинейные, и поэтому, возможно, позволяют решать те же задачи при меньшем количестве модулей.
Паде-нейрон
Паде-нейрон вычисляет произвольную дробно-линейную функцию вектора



Паде-нейрон может использоваться как обобщение нейрона типа "адалайн" в тех случаях, когда линейных функций становится недостаточно, в частности, в задачах интерполяции эмпирических зависимостей.
В случае Паде-нейрона квадратичная ошибка определяется как

и значения весовых коэффициентов уточняются по следующим формулам

Персептрон
Простой персептрон — это нейрон МакКаллока-Питса (рис.1). Весовые коэффициенты входов сумматора, на которые подаются входные сигналы




персептрона является ступенчатой, вследствие чего выходной сигнал нейрона может принимать только два значения — 0 и 1 в соответствии с правилом
 |
(1) |
или -1 и 1 в соответствии с правилом
 |
(2) |
где

 |
(3) |
В формуле (3) предполагается

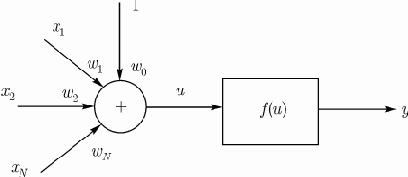
Рис. 1. Нейрон МакКаллока-Питтса
Обучение персептрона состоит в таком подборе весов




С персептроном связана задача четкого разделения двух классов по обучающей выборке, которая ставится следующим образом: имеется два набора векторов










Сигма-Пи нейроны
Выше были рассмотрены нейроны с линейной и квадратичной функциями активации. Сигма-пи нейроны являются их обобщением на случай представления функции активации u полиномом степени



где


комбинаций первых


Сигмоидальный нейрон
Нейрон сигмоидального типа имеет структуру, подобную модели МакКаллока-Питса, с той разницей, что функция активации является непрерывной и может быть выражена в виде сигмоидальной униполярной или биполярной функции. Униполярная функция, как правило, представляется формулой (рис.2)

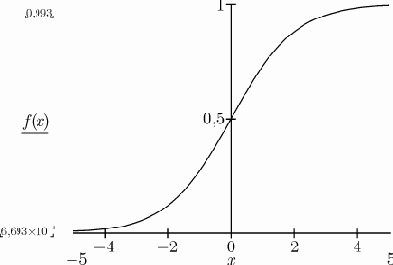
Рис. 2. Униполярная функция (? =1)
тогда как биполярная функция задается в виде (рис.3)

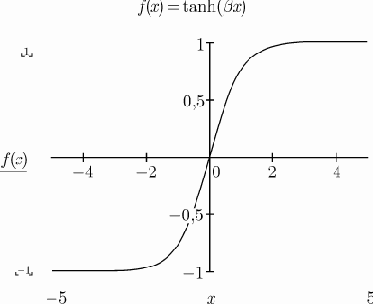
Рис. 3. Биполярная функция (?=1)
Параметр




Важным свойством сигмоидальной функции является ее дифференцируемость. Для униполярной функции имеем

тогда как для биполярной функции

Применение непрерывной функции активации позволяет использовать при обучении градиентные методы оптимизации. Проще всего реализовать метод наискорейшего спуска, в соответствии с которым уточнение вектора весов

проводится в направлении отрицательного градиента целевой функции


Компонента градиента имеет вид

где




Значения весовых коэффициентов уточняются по формуле

где

Применение градиентного метода для обучения нейрона гарантирует достижение только локального минимума. Для выхода из окрестности локального минимума результативным может оказаться обучение с моментом. В этом методе процесс уточнения весов определяется не только информацией о градиенте функции, но и предыдущим изменением весов. Подобный способ может быть задан выражением

в котором первый член соответствует обычному методу наискорейшего спуска, тогда как второй член, называемый моментом, отражает последнее изменение весов и не зависит от фактического значения градиента. Значение

выбирается из интервала (0,1).
Стохастическая модель нейрона
В стохастической модели выходное состояние нейрона зависит не только от взвешенной суммы входных сигналов, но и от некоторой случайной переменной, значения которой выбираются при каждой реализации из интервала (0,1).
В стохастической модели нейрона выходной сигнал



где


- положительная константа, которая чаще всего равна 1. Процесс обучения нейрона в стохастической модели состоит из следующих этапов:
1) расчет взвешенной суммы

для каждого нейрона сети.
2) расчет вероятности



3) генерация значения случайной переменной




При обучении с учителем по правилу Видроу-Хоффа адаптация весов проводится по формуле

Запись активации в замкнутой форме
Рассмотрим двухвходовый кубический модуль. Существует 4 значения активации






В случае


Алгоритм обучения персептрона по отдельным примерам
1. При изначально заданных значениях весов





2. Если


3. Если



где


4. Если



В обобщенной форме обучение персептрона на векторе

выражается формулой

По завершении уточнения весовых коэффициентов представляются очередной обучающий вектор




Геометрическая интерпретация линейного разделения классов
Пусть в нейроне в качестве функции активации используется ступенчатая функция (см. формулу (1) Лекции 2). Линейное разделяющее правило делит входное пространство на две части гиперплоскостью, классифицируя входные векторы как относящиеся к 1-му классу (выходной сигнал - 1) или 2-му классу (выходной сигнал - 0). Критическое условие классификации (уравнение разделяющей гиперплоскости)

В {





на вектор





Пример
В двухмерном пространстве входных сигналов уравнение гиперплоскости имеет вид

При



гиперплоскости, которая представлена на рис.1 пунктирной линией, пересекающей оси координат в точках (1.5, 0) и (0, 1.5) соответственно. Здесь:





больше



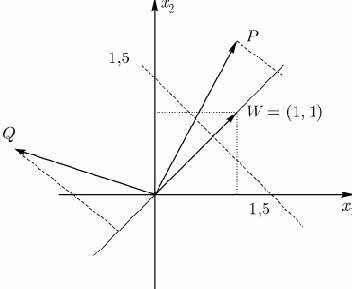
Рис. 1.
Линейное разделение классов
состоит в построении линейного решающего правила, т.е. такого вектора


— порог, что при



— ко второму.
Разделение центров масс - простейший способ построения решающего правила. Суть этого способа заключается в вычислении вектора весов персептрона по следующей формуле

где



Линейные решающие правила, построенные на основании разделения центров масс, могут ошибаться на примерах из обучающей выборки даже в тех случаях, когда существует и безошибочное линейное разделение. Однако метод центров масс полезен как средство определения начального значения вектора весов для алгоритма обучения персептрона.
Настройка весового вектора
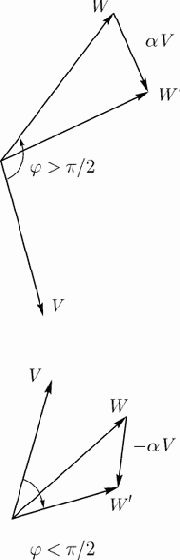
Мы требуем, чтобы вектор весов в расширенном пространстве был ортогонален решающей гиперплоскости, и плоскость проходила через начало координат. Обучающую выборку (задачник) для нейрона можно рассматривать как множество пар




Пусть для некоторого



где






на рис.2 между векторами








Предположим теперь, что









из


увеличить изображение
Рис. 2. Настройка вектора весов
Результирующая запись имеет вид:

Параметр

Алгоритм обучения нейрона (персептрона) будет иметь вид:
repeat for

begin y = h[(W,V)];

end until

Обучение по всему задачнику
Построим обучающую выборку

В обучающей выборке выделяются все




модифицируется только после проверки всей обучающей выборки:

Не требуется хранить все множество Err - достаточно накапливать сумму тех


Как показывают испытания, обучение по всему задачнику, как правило, сходится быстрее, чем обучение по отдельным примерам.
Промежуточный вариант: обучение по страницам
Обучающее множество разбивается на подмножества (страницы) и задается последовательность прохождения страниц: столько-то циклов по первой странице, потом столько-то по второй и т. д. Коррекция вектора

Метод максимума правдоподобия
Рассмотрим задачу разделения двух классов, с каждым из которых связано вероятностное распределение в пространстве векторов







" width="352" height="47">
где




где










Минимизация в формуле Байеса дает простое решающее правило:

принадлежит


для всех



знаменатель общий, то решающее правило приобретает следующий вид: выбираем то





величина


Нейрофизиологическая аналогия
Идея использования НС с квадратичными сумматорами для улучшения способности сети к обобщению базируется на хорошо известном факте индукции в естественных НС, когда возбуждение в одних областях мозга влияет на возбуждение в других. Простейшей формализацией этого является введение коэффициента, пропорционального сигналу от





где






Реализация булевых функций нейронными сетями
Простой персептрон (нейрон МакКаллока-Питса) с весовым вектором


и булеву функцию ИЛИ от двух аргументов




и булеву функцию И. Однако, персептрон не может воспроизвести даже такую простую функцию как ИСКЛЮЧАЮЩЕЕ ИЛИ. Она принимает значение единицы, когда один из аргументов равен единице (но не оба) (табл.1).
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Эту функцию реализует двухслойная нейронная сеть, представленная на рис.1 (сигнал


а вторая - уравнением

Соответствующие векторы весов имеют вид



Рис. 1. Двухслойная сеть, реализующая функцию ИСКЛЮЧАЮЩЕЕ ИЛИ
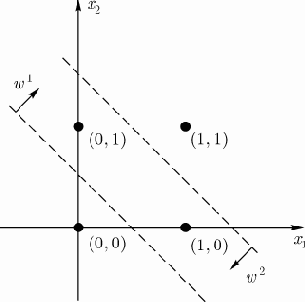
Рис. 2. Гиперплоскости, реализующие функцию ИСКЛЮЧАЮЩЕЕ ИЛИ
Выходным сигналом сети будет 1, если входные сигналы сети соответствуют точкам пространства входных сигналов, расположенным между вышеуказанными гиперплоскостями, т.е. точкам (0,1) и (1,0) (рис.2).
Выделение невыпуклых областей
Точки, не составляющие выпуклой области, не могут быть отделены от других точек пространства двухслойной сетью. Нейрон второго слоя не ограничен функцией И. Трехслойная сеть является более общей. Ограничения на выпуклость отсутствуют. Нейрон третьего слоя принимает в качестве входа набор выпуклых многоугольников, и их логическая комбинация может быть невыпуклой.
При добавлении нейронов число сторон многоугольников может неограниченно возрастать. Это позволяет аппроксимировать область любой формы с любой точностью. Вдобавок не все выходные области второго слоя должны пересекаться. Следовательно, возможно объединить различные области, выпуклые и невыпуклые, выдавая на выходе 1 всякий раз, когда входной вектор принадлежит одной из них.
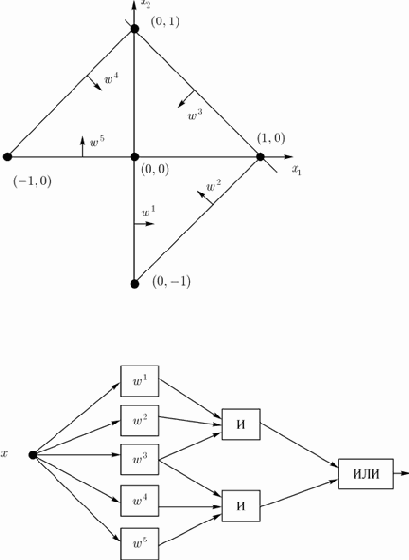
На рис.5 приведен пример выделения невыпуклой области, представленной в виде объединения двух треугольных областей. Пять нейронов первого слоя реализуют разделяющие гиперплоскости, два нейрона второго слоя реализуют трехвходовые функции И, нейрон третьего слоя реализует функцию ИЛИ. Весовые векторы, описывающие соответствующие гиперплоскости, имеют вид:


увеличить изображение
Рис. 5. Пример выделения невыпуклой области
Выделение выпуклых областей
Серьезное ограничение разделяющих поверхностей однослойными сетями можно преодолеть, добавив дополнительные слои. Например, двухслойные сети, получаемые каскадным соединением однослойных сетей, способны выполнять более общие классификации, отделяя точки, содержащиеся в выпуклых ограниченных и неограниченных областях. Область выпуклая, если для каждых двух её точек соединяющий их отрезок целиком лежит в области. Область ограничена, если её можно заключить в некоторый шар.
Выше приведен пример выделения выпуклой области двумя гиперплоскостями (реализация функции ИСКЛЮЧАЮЩЕЕ ИЛИ). Аналогично в первом слое может быть использовано 3 нейрона с дальнейшим разбиением плоскости и созданием области треугольной формы (на рис. 3, 4,

Включением достаточного числа нейронов во входной слой может быть образован выпуклый многоугольник (многогранник) желаемой формы. Так как такие многогранники образованы с помощью операций И над областями, задаваемыми разделяющими линиями (гиперплоскостями единичной размерности), то все они выпуклы.
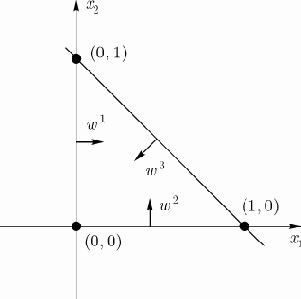
Рис. 3. Гиперплоскости, выделяющие на плоскости выпуклую (треугольную) область
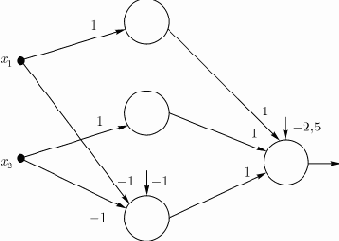
Рис. 4. Нейронная сеть, выделяющая на плоскости выпуклую (треугольную) область
Функционирование сетей
Сети периодического функционирования. Простейшие представления об этих сетях таковы.
В начальный момент состояния всех нейронов одинаковы, выходных сигналов нет. Подаются входные сигналы, определяющие активность сети (нулевой такт). Далее входные сигналы могут подаваться на каждом такте функционирования. На каждом такте могут сниматься выходные сигналы. После




Для слоистых и слоисто-полносвязных сетей начальные слои по мере срабатывания освобождаются и могут заниматься новой задачей, пока последние слои заканчивают работу над предыдущей. Сети периодического функционирования по характеру использования напоминают ЭВМ: на вопрос следует ответ, причем воспроизводимый. Иначе обстоит дело с сетями непрерывного функционирования.
Непрерывное функционирование нейронной сети более соответствует имеющимся представлениям о поведении живых существ, чем периодическое. Опыт показывает, что, чередуя циклы функционирования и обучения, для таких сетей можно получить хорошие результаты адаптации. Для непрерывного функционирования необходимы сети с циклами: полносвязные, слоисто-циклические или полносвязно-слоистые.
Интерпретация ответов сети
При интерпретации выходных сигналов сети необходимы аккуратность и порой изобретательность, ведь от этого истолкования зависят требования, которые мы предъявляем к работе НС. Удачная их формулировка может упростить обучение и повысить точность работы, неудачная — свести на нет предыдущие усилия.
Масштабирование является естественной операцией при обработке выходных сигналов. Стандартные (обезразмеренные) НС формируются так, чтобы их выходные сигналы лежали в интервалах





В задачах классификации наиболее распространено правило интерпретации "победитель забирает все": число нейронов равно числу классов, номер нейрона с максимальным сигналом интерпретируется как номер класса. К сожалению, если классов много, то этот наглядный метод является слишком расточительным, потребляет слишком много выходных нейронов.
Знаковая интерпретация требует только



Порядковая интерпретация является еще более емкой, чем знаковая. В ней с помощью


классам (а не





- наибольшему). Перестановку





Константа Липшица сигмоидальной сети
Рассмотрим слоистую сигмоидальную сеть (сеть с сигмоидальными нейронами) со следующими свойствами:
Число входных сигналов -





В этом случае оценка константы Липшица сети равна:
 |
(2) |
Формула (2) подтверждает экспериментально установленный факт, что, чем круче характеристическая функция нейрона (т.е. чем больше

Настройка нейронных сетей для решения задач
Тема данного раздела - формирование нейронных сетей для решения задач. Прежде чем приступить к поиску параметров сети, нужно поставить задачу, т.е. ответить на вопросы:
Какие сигналы сеть будет получать?Как мы будем интерпретировать сигналы, поступающие от сети?Как мы будем оценивать работу сети, если сеть обучается путем минимизации ошибок (т.е. что такое вектор ошибок и как вычисляется целевая функция — оценка функционирования сети)?
Ответы на данные вопросы воплощаются в спецустройствах или программах: в предобработчике, интерпретаторе ответов, оценке.
Итак, прежде чем формировать сеть, необходимо создать её окружение. В процессе обучения, кроме того, используются:
Обучающая выборка (система, работающая с исходными данными);Учитель, модифицирующий параметры сети;Контрастер (система, упрощающая нейронную сеть).
Оценка способности сети решить задачу
В данном разделе рассматриваются только сети, все элементы которых непрерывно зависят от своих аргументов. Предполагается, что все входные данные предобработаны так, чтобы все входные и выходные сигналы сети лежали в диапазоне приемлемых входных сигналов

Нейронная сеть вычисляет некоторую вектор-функцию


была минимальной (в идеале равна нулю), здесь




на






называется константой Липшица. Исходя из этих соображений, можно дать следующее определение сложности задачи.
Сложность аппроксимации таблично заданной функции



 |
(1) |
Оценка (1) является оценкой константы Липшица аппроксимируемой функции снизу.
Константа Липшица сети вычисляется по следующей формуле:

Для того, чтобы оценить способность сети заданной конфигурации решить задачу, необходимо оценить константу Липшица сети и сравнить ее с выборочной оценкой (1). В случае




Предобработка данных
Нормировка и центрирование данных (предобработка) используются почти всегда (кроме тех случаев, когда данные представляют собой бинарные векторы с координатами 0,1 или



Стандартные преобразования исходной выборки











Виды сетей
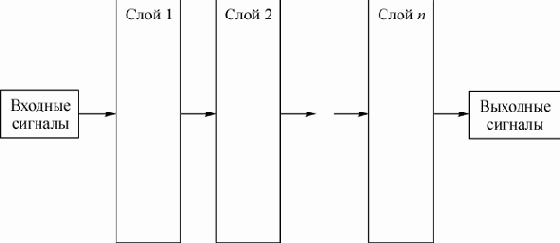
В многослойных (слоистых) сетях (рис.1) нейроны первого слоя получают входные сигналы, преобразуют их и передают нейронам второго слоя. Далее срабатывает второй слой и т.д., до



увеличить изображение
Рис. 1. Многослойная (слоистая) сеть
Монотонные слоистые сети - частный случай слоистых сетей с дополнительными условиями на связи и элементы. Каждый слой, кроме выходного, разбит на два блока - возбуждающий и тормозящий. Связи между слоями также подразделяются на два типа - возбуждающие (с положительными весами) и тормозящие (с отрицательными весами). Если от блока



является монотонной неубывающей функцией любого выходного сигнала блока


В полносвязной сети каждый нейрон передает свой выходной сигнал остальным нейронам, в том числе и самому себе. Выходными сигналами сети могут быть все или некоторые выходные сигналы нейронов после нескольких циклов функционирования сети. Все входные сигналы подаются всем нейронам. Для полносвязной сети входной сумматор нейрона фактически распадается на два: первый вычисляет линейную функцию от входных сигналов сети, второй - линейную функцию от выходных сигналов других нейронов, полученных на предыдущем шаге. Примером полносвязной сети является сеть Хопфилда.
Слоисто-циклические (рекуррентные) сети отличаются тем, что слои замкнуты в кольцо - последний передает свои выходные сигналы первому.
Все слои равноправны и могут как получать входные сигналы, так и выдавать выходные. Такие сети до получения ответа могут функционировать неограниченно долго, так же, как и полносвязные.
Слоисто-полносвязные сети состоят из слоев, каждый из которых, в свою очередь, представляет собой полносвязную сеть. При функционировании сигналы передаются от слоя к слою, и происходит обмен сигналами внутри слоя. В каждом слое процесс протекает следующим образом: прием сигналов с предыдущего слоя (или входных сигналов сети), обмен сигналами внутри слоя, передача последующему слою (или на выход). Подобные сети до получения ответа функционируют определенное число тактов, соответствующее количеству слоев, так же, как и слоистые сети.
Полносвязно-слоистые сети по структуре такие же, как и предыдущие, но функционируют по-другому. В них не разделяются фазы обмена внутри слоя и передачи следующему: на каждом такте нейроны всех слоев принимают сигналы от нейронов как своего, так и предыдущего, после чего передает сигналы как внутри слоя, так и последующему (или на выход). До получения ответа подобные сети могут функционировать неограниченно долго, так же, как и полносвязные.
Алгоритм обратного распространения ошибки
Возьмем двухслойную сеть (рис. 1) (входной слой не рассматривается). Веса нейронов первого (скрытого) слоя пометим верхним индексом (1), а выходного слоя - верхним индексом (2). Выходные сигналы скрытого слоя обозначим







Цель обучения состоит в подборе таких значений весов








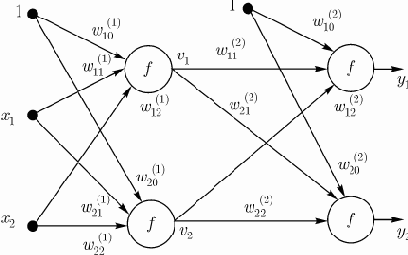
Рис. 1. Пример двухслойной нейронной сети
В выходном слое


Из формулы следует, что на значение выходного сигнала влияют веса обоих слоев, тогда как сигналы, вырабатываемые в скрытом слое, не зависят от весов выходного слоя.
Основу алгоритма обратного распространения ошибки составляет целевая функция, формулируемая, как правило, в виде квадратичной суммы разностей между фактическими и ожидаемыми значениями выходных сигналов. Для обучающей выборки, состоящей из


Минимизация целевой функции достигается уточнением вектора весов (обучением) по формуле

где
 |
(1) |




 |
(2) |
4. Описанный процесс следует повторить для всех обучающих примеров задачника, продолжая его вплоть до выполнения условия остановки алгоритма. Действие алгоритма завершается в момент, когда норма градиента упадет ниже априори заданного значения, характеризующего точность процесса обучения.
Руководствуясь рис. 2, можно легко определить все компоненты градиента целевой функции, т.е. все частные производные функции



Так, например, чтобы посчитать производную




и

и затем сложить эти произведения и результат умножить на

и

Таким образом, получим



Методы инициализации весов
Обучение нейронных сетей представляет собой трудоемкий процесс, далеко не всегда дающий ожидаемые результаты. Проблемы возникают из-за нелинейных функций активации, образующих многочисленные локальные минимумы, к которым может сводиться процесс обучения. Применение методов глобальной оптимизации уменьшает вероятность остановки процесса обучения в точке локального минимума, однако платой за это становится резкое увеличение трудоемкости и длительности обучения. Для правильного подбора управляющих параметров требуется большой опыт.
На результаты обучения огромное влияние оказывает подбор начальных значений весов сети. Выбор начальных значений, достаточно близких к оптимальным, значительно ускоряет процесс обучения. К сожалению, не существует универсального метода подбора весов, который бы гарантировал нахождение наилучшей начальной точки для любой решаемой задачи.
Неправильный выбор диапазона случайных значений весов может вызвать слишком раннее насыщение нейронов, в результате которого, несмотря на продолжающееся обучение, среднеквадратичная погрешность будет оставаться практически постоянной. Это означало бы попадание в седловую зону целевой функции вследствие слишком больших начальных значений весов. При этом взвешенная сумма входных сигналов нейрона может иметь значение, соответствующее глубокому насыщению сигмоидальной функции активации, и поляризация насыщения будет обратна ожидаемой. Значение возвратного сигнала, генерируемое в методе обратного распространения, пропорционально величине производной от функции активации и в точке насыщения близко нулю. Поэтому изменения значений весов, выводящие нейрон из состояния насыщения, происходят очень медленно. Процесс обучения надолго застревает в седловой зоне. Нейрон, остающийся в состоянии насыщения, не участвует в преобразовании данных, сокращая таким образом эффективное количество нейронов в сети. В итоге процесс обучения чрезвычайно замедляется, поэтому состояние насыщения отдельных нейронов может длиться практически непрерывно вплоть до исчерпания лимита итераций.
Удаление стартовой точки активации нейронов от зоны насыщения достигается путем ограничения диапазона случайных значений. Почти все оценки нижней и верхней границ диапазона допустимых значений лежат в интервале (0,1). Хорошие результаты дает равномерное распределение весов, нормализованное для каждого нейрона по амплитуде



Одномерная оптимизация
Все пошаговые методы оптимизации состоят из двух важнейших частей:
выбора направления, выбора шага в данном направлении (подбор коэффициента обучения).
Методы одномерной оптимизации дают эффективный способ для выбора шага.
В простейшем случае коэффициент обучения фиксируется на весь период оптимизации. Этот способ практически используется только совместно с методом наискорейшего спуска. Величина подбирается раздельно для каждого слоя сети по формуле

где


Более эффективный метод основан на адаптивном подборе коэффициента





Для ускорения процесса обучения следует стремиться к непрерывному увеличению


Если погрешности на









где



- коэффициент увеличения

Наиболее эффективный, хотя и наиболее сложный, метод подбора коэффициентов обучения связан с направленной минимизацией целевой функции в выбранном направлении




Поиск минимума основан на полиномиальной аппроксимации целевой функции. Выберем для аппроксимации многочлен второго порядка

где






Соответствующие этим точкам значения целевой функции

обозначим как
 |
(5) |
Коэффициенты



рассчитываются в соответствии с решением системы уравнений (5).
Для определения минимума многочлена







Одношаговый квазиньютоновский метод и сопряженные градиенты
В тех случаях, когда является положительно определенной матрица

вторых производных оценки


С использованием этой формулы квадратичные формы минимизируются за один шаг, однако, применять эту формулу трудно по следующим причинам:
Время. Поиск всех вторых производных функции






Для преодоления этих трудностей разработана масса методов. Идея квазиньютоновских методов с ограниченной памятью состоит в том, что поправка к направлению наискорейшего спуска отыскивается как результат действия матрицы малого ранга. Сама матрица не хранится, а её действие на векторы строится с помощью скалярных произведений на несколько специально подобранных векторов.
Простейший и весьма эффективный метод основан на














где



Если одномерную оптимизацию в поиске шага проводить достаточно точно, то новый градиент




Это - формула метода сопряженных градиентов (МСГ), которому требуется достаточно аккуратная одномерная оптимизация при выборе шага.
В описанных методах предполагается, что начальное направление спуска



Особенности задачи оптимизации, возникающей при обучении нейронных сетей
Задачи оптимизации нейронных сетей имеют ряд специфических ограничений. Они связаны с огромной размерностью задачи обучения. Число параметров может достигать



Ограничение по памяти. Пусть



Партан-методы
Для исправления недостатков наискорейшего спуска разработаны итерационный и модифицированный партан-методы.
Итерационный партан-метод (





раз. После





Модифицированный партан-метод требует запоминания дополнительных параметров. Он строится следующим образом. Из

















Учет ограничений при обучении
Для параметров сети возможны ограничения простейшего вида:

Они вводятся из различных соображений: чтобы избежать слишком крутых или, наоборот, слишком пологих характеристик нейронов, чтобы предотвратить появления слишком больших коэффициентов усиления сигнала на синапсах и т.п.
Учесть ограничения можно, например, методом штрафных функций либо методом проекций:
Использование метода штрафных функций означает, что в оценку

добавляется штрафы за выход параметров из области ограничений. В~градиент





Практика показывает, что проективный метод не приводит к затруднениям. Обращение со штрафными функциями менее успешно. Далее будем считать, что ограничения учтены одним из методов, и будем говорить об обучении как о безусловной минимизации.
Универсальный путь обучения
Существует универсальный путь обучения нейронных сетей - минимизация оценки как неявно заданной функции параметров сети. При реализации этого подхода предполагается, что:
задана обучающая выборка, состоящая из векторов входных сигналов





После подготовки (создание обучающей выборки, выбор функции оценки, предобработка входных данных и т.п.), предшествующей обучению, имеем способ вычисления некоторой функции

Выбор направления минимизации
Пусть задано начальное значение вектора параметров



Наиболее очевидный выбор направления



Выберем на каждом шаге это направление, затем проведем одномерную оптимизацию, потом снова вычислим градиент

Другой способ - случайный выбор направления

Алгоритмы имитации отжига
Метод имитации отжига основан на идее, заимствованной из статистической механики. Он отражает поведение расплавленного материала при отвердевании с применением процедуры отжига (управляемого охлаждения) при температуре, последовательно понижаемой до нуля.
В процессе медленного управляемого охлаждения, называемого отжигом, кристаллизация расплава сопровождается глобальным уменьшением его энергии, однако допускаются ситуации, в которых она может на какое-то время возрастать (в частности, при подогреве расплава для предотвращения слишком быстрого его остывания). Благодаря допустимости кратковременного повышения энергетического уровня, возможен выход из ловушек локальных минимумов энергии, которые возникают при реализации процесса. Только понижение температуры до абсолютного нуля делает невозможным какое-либо самостоятельное повышение энергетического уровня расплава.
Метод имитации отжига представляет собой алгоритмический аналог физического процесса управляемого охлаждения. Классический алгоритм имитации отжига можно описать следующим образом:
Запустить процесс из начальной точки




















Наибольшего ускорения имитации отжига можно достичь путем замены случайных начальных значений весов

Метод имитации отжига оказывается особенно удачным для полимодальных комбинаторных проблем с очень большим количеством возможных решений, например, для машины Больцмана, в которой каждое состояние системы считается допустимым. При решении наиболее распространенных задач обучения многослойных нейронных сетей наилучшие результаты в общем случае достигаются применением стохастически управляемого метода повторных рестартов совместно с детерминированными алгоритмами локальной оптимизации.
Четыре типа устойчивости
Навыки обучения нейрокомпьютера должны быть устойчивы к возмущению различных типов. Разработчики нейрокомпьютеров выделяют четыре типа устойчивости:
к случайным возмущениям входных сигналов;к флуктуациям параметров сети;к разрушению части элементов сети;к обучению новым примерам.
В конкретных ситуациях необходимо доопределять возмущения, по отношению к которым нужно вырабатывать устойчивость. Например, при распознавании визуальных образцов можно выделить несколько разновидностей возмущений входного сигнала: прибавление случайного сигнала (шум фона), затенение части исходного изображения, искажение изображения некоторыми преобразованиями.
Для выработки устойчивости первых трех типов полезны генераторы случайных искажений. Для устойчивости 1-го типа генератор искажений производит возмущение входных сигналов и тем самым преобразует обучающей пример. Для устойчивости 2-го типа генератор искажений меняет случайным образом параметры сети в заданных пределах, а для устойчивости 3-го типа - удаляет случайно выбранную часть сети, состоящую из заданного количества элементов (нейронов, синапсов).
В существенной конкретизации нуждается четвертый тип устойчивости, т.к. трудно представить себе устойчивость к обучению любому новому примеру. Если принять гипотезу, что обучение новым примерам будет действовать на старые навыки так же, как случайный сдвиг параметров, то получается, что выработка устойчивости 2-го типа является средством для обучения устойчивости 4-го типа. Другое средство - выработка устойчивости к обучению отдельным примерам, уже входящим в задачник. Это свойство устойчивости 1-го типа состоит в том, что обучение до минимума оценки по любому (одному) из обучающих примеров не разрушает навыка решения остальных. Возмущение здесь состоит в изменении процесса обучения.
Для выработки устойчивости 1-го типа примеры предъявляются сети не все сразу, а по одному, и сеть учится каждому из них до предела. Для выработки важнейшей устойчивости 4-го типа такая периодически производимая "порча" процесса обучения может быть полезной. Опыт показывает, что обучение позволяет выработать устойчивость к весьма сильным возмущением. Так, в задачах распознавания визуальных образов уровень шума на выходе мог в несколько раз превосходить общую интенсивность сигнала, случайный сдвиг параметров - достигать 0.5-0.7 их предельного значения, разрушение - 30-50\% элементов. И, тем не менее, обученная сеть делает не более 10\% ошибок!
Генетические алгоритмы
Генетические алгоритмы имитируют процессы наследования свойств живыми организмами и генерируют последовательности новых векторов


На начальной стадии выполнения генетического алгоритма случайным образом инициализируется определенная популяция хромосом (векторов

Селекция хромосом для спаривания (необходимого для создания нового поколения) может основываться на разных принципах. Одним из наиболее распространенных считается принцип элитарности, в соответствии с которым наиболее приспособленные (в смысле целевой функции) хромосомы сохраняются, а наихудшие отбраковываются и заменяются вновь созданным потомством, полученным в результате скрещивания пар родителей.
Существует огромное множество методов скрещивания, начиная с полностью случайного. При взвешенно-случайном скрещивании учитывается информация о текущем значении целевой функции. Отбор может происходить по принципу рулетки; при этом площадь сегмента колеса рулетки, сопоставленного конкретной хромосоме, пропорциональна величине ее функции приспособленности


- ее целевая функция.
Процесс скрещивания основан на рассечении пары хромосом на две части с последующим обменом этих частей в хромосомах родителей (рис. 1). Место рассечения также выбирается случайным образом. Количество новых потомков равно количеству отбракованных в результате селекции (размер популяции остается неизменным). Признается допустимым перенос в очередное поколение некоторых случайно выбранных хромосом вообще без скрещивания.
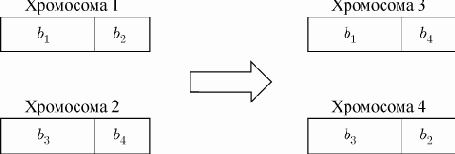
Рис. 1. Процесс скрещивания
Последняя генетическая операция - это мутация. При двоичном кодировании мутация состоит в инверсии случайно выбранных битов.
При кодировании векторов десятичными числами мутация заключается в замене значения какого-либо элемента вектора другим случайно выбранным значением. Мутация обеспечивает защиту как от слишком быстрого завершения алгоритма (в случае выравнивания значений всех хромосом и целевой функции), так и от представления в какой-либо конкретной позиции всех хромосом одного и того же значения. Однако необходимо иметь в виду, что случайные мутации приводят к повреждению уже частично приспособленных векторов. Обычно мутации подвергается не более


Доказано, что каждое последующее поколение, сформированное селекцией, скрещиванием и мутацией, имеет статистически лучшие средние показатели приспособленности (меньшие значения целевой функции).
В качестве окончательного решения принимается наиболее приспособленная хромосома, имеющая минимальное значение целевой функции. Генетический процесс завершается либо в момент генерации удовлетворяющего нас решения, либо при выполнении максимально допустимого количества итераций. При реализации генетического процесса отслеживается, как правило, не только минимальное значение целевой функции, но и среднее значение по всей популяции хромосом, а также их вариации. Решение об остановке алгоритма может приниматься и в случае отсутствия прогресса минимизации, определяемого по изменениям названных характеристик.
Элементы глобальной оптимизации
Все представленные ранее методы обучения нейронных сетей являются локальными. Они ведут к одному из локальных минимумов целевой функции, лежащему в окрестности точки начала обучения. Только в ситуации, когда значение глобального минимума известно, удается оценить, находится ли найденный локальный минимум в достаточной близости от искомого решения. Если локальное решение признается неудовлетворительным, следует повторить процесс обучения при других начальных значениях весов и с другими управляющими параметрами. Можно либо проигнорировать полученное решение и начать обучение при новых (как правило, случайных) значениях весов, либо изменить случайным образом найденное локальное решение (встряхивание весов) и продолжить обучение сети.
При случайном приращении весов переход в новую точку связан с определенной вероятностью того, что возобновление процесса обучения выведет поиск из "сферы притяжения" локального минимума.
При решении реальных задач в общем случае даже приблизительная оценка глобального минимума оказывается неизвестной. По этой причине возникает необходимость применения методов глобальной оптимизации. Рассмотрим три из разработанных подходов к глобальной оптимизации: метод имитации отжига, генетические алгоритмы и метод виртуальных частиц.
Метод виртуальных частиц
Метод виртуальных (случайных) частиц может надстраиваться почти над любым методом оптимизации. Он создан для:
повышения устойчивости обученных сетей;вывода сетей из возникающих при обучении локальных минимумов оценки.
Основная идея метода - использование случайных сдвигов аргумента и суммирование полученных значений функции для усреднения. Ожидается, что в результате уменьшится влияние рельефа минимизируемой функции на процесс минимизации и откроется более прямой путь к её глобальному минимуму.
Метод случайных частиц состоит в том, что к оптимизируемой точке (частице) добавляется несколько других, траектории которых получаются из траектории данной частицы сдвигом на случайный вектор. Эти "виртуальные" частицы время от времени уничтожаются и рождаются новые. Спуск (минимизация) строится так, чтобы уменьшилось значение суммы значений оптимизируемой функции в указанных точках.
Рассмотрим один из вариантов алгоритма виртуальных частиц. Пусть требуется найти минимум функции




Начальное положение основной частицы -




 |
(1) |
и её положение задается вектором







Алгоритм локальной оптимизации может быть выбран любой - от наискорейшего спуска и партан-методов до метода сопряженных градиентов. Выбор



для каждой координаты вектора





В методе виртуальных частиц возникает важный вопрос: когда уничтожать имеющиеся виртуальные частицы и порождать новые?
Есть три варианта:
Функция

Первый способ наиболее консервативен. Он долго сохраняет все достоинства и недостатки предшествующего спуска, хотя направление движения может существенно измениться при порождении новых виртуальных частиц.
Третий способ вносит случайный процесс внутрь базового алгоритма, в результате возможны колебания даже при одномерной оптимизации. Его преимущество - экономия памяти.
Наиболее перспективным представляется второй способ. Он, с одной стороны, не разрушают базового алгоритма, а с другой - за счет многократного порождения виртуальных частиц позволяет приблизиться к глобальному множеству. Метод виртуальных частиц имеет все достоинства методов глобальной оптимизации, не использующих случайные возмущения, но лишен многих их недостатков.
Хорошие результаты обучения приносит объединение алгоритмов глобальной оптимизации с детерминированными методами локальной оптимизации. На первом этапе обучения сети применяется выбранный алгоритм глобальной оптимизации, а после достижения целевой функцией определенного уровня включается детерминированная оптимизация с использованием какого-либо локального алгоритма.

